1. 最大公约数和最小公倍数
1 int gcd(int a,int b){ 2 if(b==0) return a; 3 return gcd(b,a%b); 4 } 5 6 int lcm(int a, int b){ 7 return a/gcd(a,b)*b; 8 9 }
2.
P1313 计算系数
思路:杨辉三角+二项式定理
二项式定理
公式: (a+b)^n = C(n,0) a^n + C(n,1) a^(n-1) b +...+ C(n,i) a^(n-i) b^i +...+ C(n,n) b^n
注:C(n,i)表示从n个元素中任取i个的组合数=n!/(n-i)!i!
系数性质:
①对称性:
②增减性和最大值:先增后减
证明:
1、Cn0+Cn1+Cn2…+Cnk+…+Cnn=2^n
2、Cno-Cn1+Cn2-Cn3+……(-1)^nCnn=0
3、Cn0+Cn2+Cn4+……=Cn1+Cn3+Cn5+……=2^(n-1)
由(a+b)^n=C(n,0)a^n+C(n,1)a^(n-1)*b+C(n,2)a^(n-2)*b^2+...+C(n,n)b^n
当a=b=1时,代入二项式定理可证明1
当a=1,b=-1时代入二项式定理可证明2
由①+②得:2(Cn0+Cn2+Cn4+……)=2^n
所以 Cn0+Cn2+Cn4+……=2^(n-1)
由①-②得:2(Cn1+Cn3+Cn5+……)=2^n
所以 Cn1+Cn3+Cn5+……=2^(n-1)
可知 Cn0+Cn2+Cn4+……=Cn1+Cn3+Cn5+……=2^(n-1)可证明3
注:组合数的性质:
⑴:C(n,m)=C(n,n-m)
⑵:C(n+1,m)=C(n,m)+C(n,m-1)
⑶:C(n,0)=C(n,n)=1
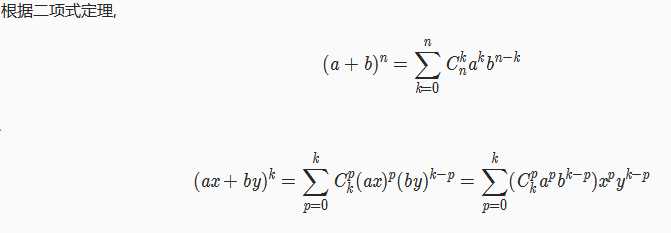
#include<cstdio>
const int N=1010;
const int mod=10007;
using namespace std;
int f[N][N],a,b,k,n,m;
int ksm(long x,long y){//int ->80 玄学
long ret=1;
while(y){
if(y%2==1) ret=ret*x%mod;
x=x*x%mod;
y/=2;
}
return ret;
}// x^y
int main()
{
scanf("%d%d%d%d%d",&a,&b,&k,&n,&m);
f[0][0]=1;
for(int i=1;i<=k;i++)
f[i][0]=1,f[i][i]=1;
for(int i=1;i<=k;i++)
for(int j=1;j<i;j++)
f[i][j]=(f[i-1][j]+f[i-1][j-1])%mod;
//杨辉三角 计算f(k,m)
printf("%d",((f[k][m]*ksm(b,m))%mod*ksm(a,n))%mod);
// 计算f(k,m)* a^m * b^(k-m)
return 0;
}
原文:https://www.cnblogs.com/RR-Jin/p/11338262.html