希尔排序算法思想
算法图解
使用希尔排序对4,5,8,2,3,9,7,1进行排序,此时采用增量序列为{1,2,3},
当增量为3时:
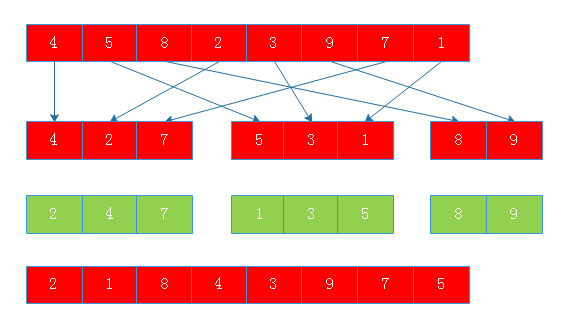
当增量为2时:
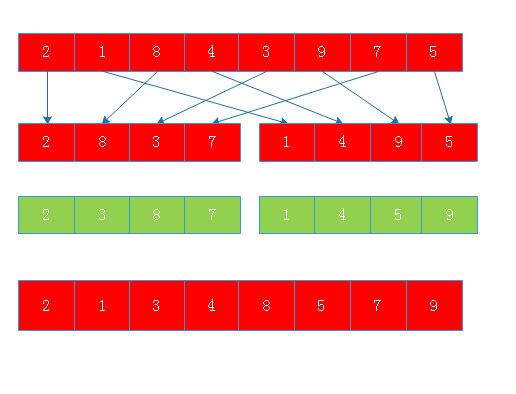
当增量为1时:
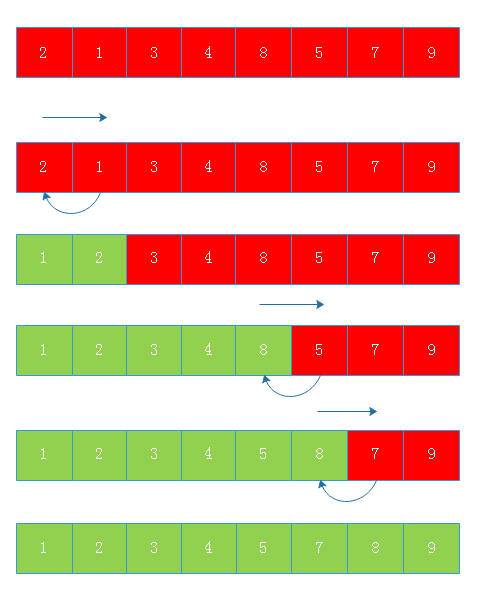
可以看出当增量为1时,待排序元素已经大致有序,此时进行一次插入排序即可完成排序
增量序列的选取
希尔排序是否高效取决于增量序列的选取,计算机科学家Knuth在《the art of compute programming》
中提出当相邻增量之间的比例为1:3时效果还行,也就是增量序列为{1,4,13,40,121,364,1093,.....}时
希尔排序和直接插入排序:
希尔排序是插入排序的扩展,插入排序每插入一次都要将插入位置以及它后面的元素整体向后进行一次平移,
例如,如果升序排序时,如果最小的元素在尾部,那么就需要N次才能将其插入到数组的首元素位置,这期间要
进行多次移动,希尔排序通过允许非相邻的等间距元素进行交换来减少插入排序频繁挪动元素的弊端。
bool ShellSort(int * pUnSortAry, int nSize) { if (pUnSortAry == nullptr || nSize <= 0) { return false; } int nGrp = 0; for (nGrp = 1; nGrp <= (nSize - 1) / 9; nGrp = nGrp * 3 + 1); for ( ; nGrp >0; nGrp/=3) { for (int iIndex = nGrp; iIndex < nSize; iIndex++) { int nTemp = pUnSortAry[iIndex]; int jIndex = iIndex - nGrp; for (; jIndex >= 0 && pUnSortAry[jIndex] > nTemp; jIndex -= nGrp) { pUnSortAry[jIndex+nGrp] = pUnSortAry[jIndex]; } pUnSortAry[jIndex+nGrp] = nTemp; } } return false; }
测试代码:
int main() { srand(time(NULL)); int nArry[30] = { 0 }; for (int jIndex = 0; jIndex < 10; jIndex++) { for (int iIndex = 0; iIndex < sizeof(nArry) / sizeof(nArry[0]); iIndex++) { nArry[iIndex] = rand() % 150; } printf("排序前:"); PrintData(nArry, sizeof(nArry) / sizeof(nArry[0])); ShellSort(nArry, sizeof(nArry) / sizeof(nArry[0])); printf("排序后:"); PrintData(nArry, sizeof(nArry) / sizeof(nArry[0])); } return 0; }
测试结果:
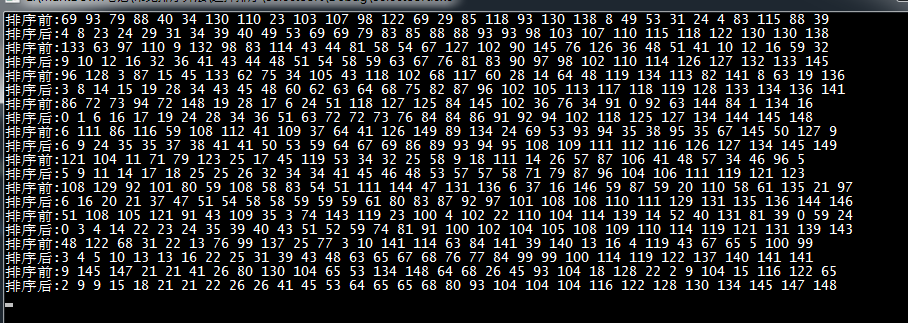
希尔排序是将等距离的元素分为一组,相同的元素可能会被分到不同的组,在一个分组中的插入排序是文档的,
但是在多个分组多次插入排序的情况下可能会改变相同元素的相对位置,所以希尔排序是不稳定的排序
原文:https://www.cnblogs.com/UnknowCodeMaker/p/11343621.html