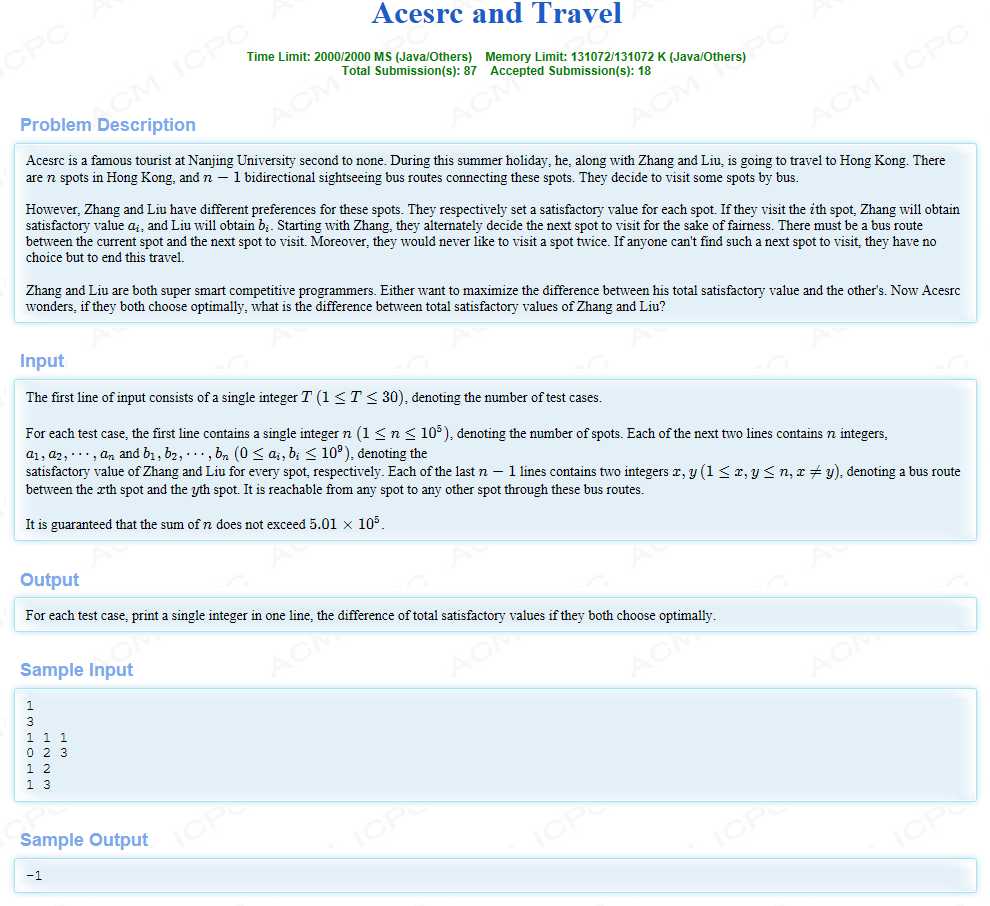
题目大意:给你一棵树,每个节点有一个权值,Alice和Bob进行博弈,起点由Alice确定,确定后交替选择下一个点,Alice目标是最终值尽可能大,Bob目标是尽可能小
题解:很明显是树形DP,那么考虑如何dp
设F[i][0/1]表示第i个点先手选/后手选的答案
那么不难想到
F[i][0]=max(F[j][1])+v[i]
F[i][1]=min(F[j][0])+v[i]
一次以1为根进行dfs可以求出选择1为根时的答案,此时考虑换根
换根时将换根前的所有状态保存下来,dfs下去之后求出其子树答案后将状态复原
换根时有两种情况,1、原根的答案是新根推过来的。2、原根的答案不是从新根推过来的
对于第二种情况很简单,我们只需要把原根当做新根的子树然后进行转移即可
考虑第一种情况,将原根变为儿子之后,其F值由除新根之外的所有儿子转移而来
于是很容易想到在原有保存最大值(最小值)的基础上再保存次大值(次小值),这样就可以O(1)更新原根的答案了
更新完后就和第二种情况一样了
代码:
#include<iostream> #include<cstdio> #include<cstdlib> #include<cstring> #include<string> #define ll long long #define INF 1e18 using namespace std; int T,n; ll v[100001],f[100001][2]; ll mx[100001][2],mn[100001][2]; ll ans; int mxbh[100001],mnbh[100001]; struct node { int x,y; }tr[100001*2]; int hd[100001],nxt[100001*2],rn; void build(int x,int y){tr[++rn]=(node){x,y};nxt[rn]=hd[x];hd[x]=rn;} void init() { rn=0; memset(f,0,sizeof(f)); memset(hd,0,sizeof(hd)); memset(nxt,0,sizeof(nxt)); } void dfs(int now,int last) { int t1=hd[now],t2; mx[now][0]=mx[now][1]=-INF; mn[now][0]=mn[now][1]=INF; mxbh[now]=0;mnbh[now]=0; while(t1) { t2=tr[t1].y; if(t2!=last) { dfs(t2,now); if(f[t2][1]>=mx[now][0]){mx[now][1]=mx[now][0];mx[now][0]=f[t2][1];mxbh[now]=t2;} else if(f[t2][1]>mx[now][1])mx[now][1]=f[t2][1]; if(f[t2][0]<=mn[now][0]){mn[now][1]=mn[now][0];mn[now][0]=f[t2][0];mnbh[now]=t2;} else if(f[t2][0]<mn[now][1])mn[now][1]=f[t2][0]; } t1=nxt[t1]; } if(mx[now][0]==-INF)mx[now][0]=0; if(mn[now][0]==INF)mn[now][0]=0; //printf("%d:%lld %lld %lld\n",now,mx[now][0],mn[now][0],v[now]); f[now][0]=mx[now][0]+v[now]; f[now][1]=mn[now][0]+v[now]; //printf("%d %lld %lld %lld\n",now,f[now][1],max1,v[now]); } void dfs2(int now,int last) { ans=max(ans,f[now][1]); //printf(" %d\n",now); //for(int i=1;i<=n;i++)printf("%lld %lld:%d %d\n",f[i][0],f[i][1],mxbh[i],mnbh[i]); //printf(" %lld %lld|%lld %lld\n",mx[now][0],mx[now][1],mn[now][0],mn[now][1]); //printf("\n"); int t1=hd[now],t2; ll fi0,fi1,fj0,fj1,tv,mxj0,mxj1,mnj0,mnj1; int mxbhi,mxbhj,mnbhi,mnbhj; while(t1) { t2=tr[t1].y; if(t2!=last) { fi0=f[now][0];fi1=f[now][1]; fj0=f[t2][0];fj1=f[t2][1]; mxbhi=mxbh[now];mnbhi=mnbh[now]; mxbhj=mxbh[t2];mnbhj=mnbh[t2]; if(mxbh[now]==t2) { tv=v[now]; if(mx[now][1]!=-INF)tv+=mx[now][1]; f[now][0]=tv; } if(mnbh[now]==t2) { tv=v[now]; if(mn[now][1]!=INF)tv+=mn[now][1]; f[now][1]=tv; } mxj0=mx[t2][0];mxj1=mx[t2][1]; mnj0=mn[t2][0];mnj1=mn[t2][1]; if(mxbhj==0)mx[t2][0]=-INF; if(mnbhj==0)mn[t2][0]=INF; if(f[now][1]>=mx[t2][0]){mx[t2][1]=mx[t2][0];mx[t2][0]=f[now][1];mxbh[t2]=now;} else if(f[now][1]>mx[t2][1])mx[t2][1]=f[now][1]; if(f[now][0]<=mn[t2][0]){mn[t2][1]=mn[t2][0];mn[t2][0]=f[now][0];mnbh[t2]=now;} else if(f[now][0]<mn[t2][1])mn[t2][1]=f[now][0]; f[t2][0]=mx[t2][0]+v[t2]; f[t2][1]=mn[t2][0]+v[t2]; dfs2(t2,now); f[now][0]=fi0;f[now][1]=fi1; f[t2][0]=fj0;f[t2][1]=fj1; mx[t2][0]=mxj0;mx[t2][1]=mxj1; mn[t2][0]=mnj0;mn[t2][1]=mnj1; mxbh[now]=mxbhi;mnbh[now]=mnbhi; mxbh[t2]=mxbhj;mnbh[t2]=mnbhj; } t1=nxt[t1]; } } int main() { scanf("%d",&T); int a,b; while(T--) { init(); scanf("%d",&n); for(int i=1;i<=n;i++)scanf("%lld",&v[i]); for(int i=1;i<=n;i++){scanf("%d",&a);v[i]-=a;} for(int i=1;i<n;i++) { scanf("%d%d",&a,&b); build(a,b);build(b,a); } memset(f,0,sizeof(f)); dfs(1,0); ans=-INF; //for(int i=1;i<=n;i++)printf("%lld %lld/%lld %lld:%d %d %lld %lld\n",mx[i][0],mx[i][1],mn[i][0],mn[i][1],mxbh[i],mnbh[i],f[i][0],f[i][1]); dfs2(1,0); //ans=-INF; //for(int i=1;i<=n;i++)ans=max(ans,f[i][1]); //for(int i=1;i<=n;i++)printf("%lld %lld:%d %d\n",f[i][0],f[i][1],mxbh[i],mnbh[i]); printf("%lld\n",ans); } return 0; }
心得:典型的树形DP的题目,换根时的操作还需要更多练习熟练
【HDU6662】Acesrc and Travel【树形DP】
原文:https://www.cnblogs.com/worcher/p/11353849.html