正态分布密度函数是:
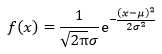
若随机变量X服从一个数学期望为μ、方差为σ2的正态分布,记为N(μ,σ2)。当μ=0,σ2=1是,称为标准正态分布。不需要记住这个复杂的公式,知道它的意义即可,在使用时可以随时查阅。
在研究正态分布时,我们认为每个样本都是等权的,因此μ是随机变量的均值,控制了曲线的位置,σ2控制了曲线的陡峭程度:
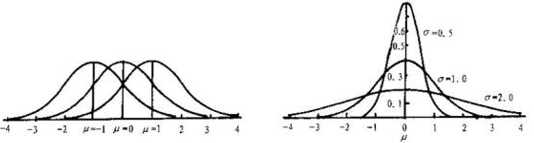
σ2越小,样本越靠近μ:
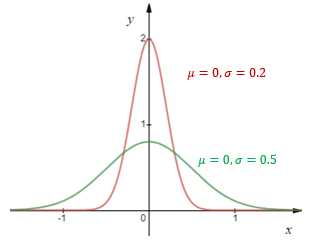
在上图中,当σ=0.2时,曲线更陡峭,倒钟更窄,样本更向μ处集中。
随机变量X服从正态分布:
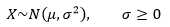
如果有n个可观察样本,根据最大似然函数的公式:
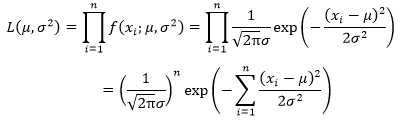
其中:
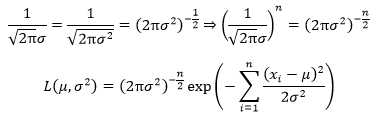
取对数似然函数,并根据对数计算公式继续化简:

由①可以得知:
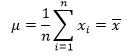
现在可以得出最终结论:
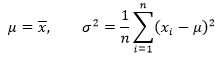
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公作者众号“我是8位的”

原文:https://www.cnblogs.com/bigmonkey/p/11353662.html