(1)到底是深层还是浅层是一个相对的概念,不必太纠结,以下是一个四层的深度神经网络:
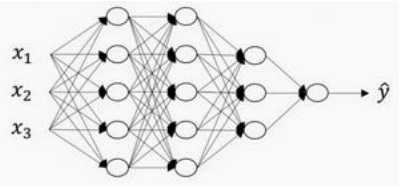
(2)一些符号定义:
a[0]=x(输入层也叫做第0层)
L=4:表示网络的层数
g:表示激活函数
第l层输出用a[l],最终的输出用a[L]表示
n[1]=5:表示第一层有五个神经元,第l层神经元个数用n[l]表示
(1)前向传播:输入a[l-1],输出是a[l],缓存为z[l],步骤如下:(下面第一个式子应该是a[l-1])
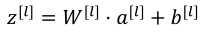
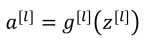
向量化:
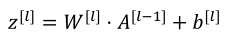
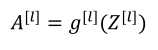
(2)反向传播:输入da[l],输出da[l-1],dw[l],db[l]
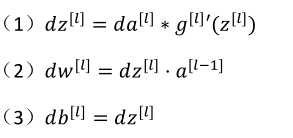
(4)da[l-1]=w[l]T·dz[l]
由第四个式子带入到第一各式子中得
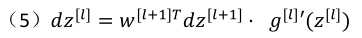
向量化:
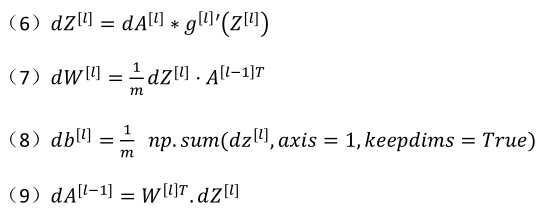
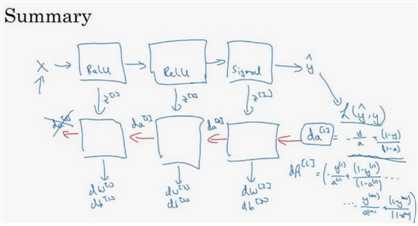
(3)总结:第一层可能是Relu激活函数,第二层为另一个Relu函数,第三层可能是sigmoid函数(如果做二分类的话),输出值为a[L],用来计算损失,这样就可以以向后迭代进行反向传播就到来求dw[3],db[3],dw[2],db[2],dw[1],db[1].在计算的时候,缓存会把z[1]z[2]z[3]传递过来,然后回传da[2],da[1],可以用来计算da[0],但是不会使用它。整个过程如下图所示
(1)前向传播归纳为:
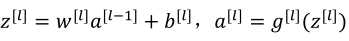
向量化实现过程:
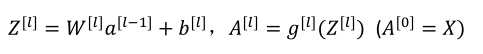
(1)w的维度是(下一层的维数,上一层的维数),即w[l]:(n[l],n[l-1])
(2)b的维度时(下一层的维数,1)
(3)z[l],a[l]:(n[l],1)
(4)dw[l]和w[l]维度相同,db[l]和b[l]维度相同,且w,b向量化维度不变,但z,a以及x的维度会向量化后发生改变。
向量化后:
Z[l]:(n[l],m),A[l]同Z[l]
增加网络的深度比广度更有效。
(1)针对一层的正向和反向传播:
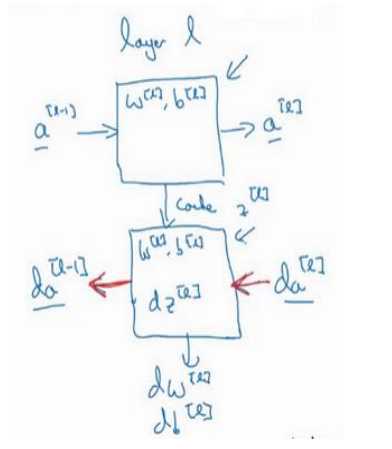
(2)整个过程示意图:
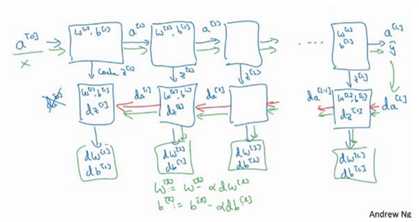
(1)W,b是参数
(2)学习率、迭代次数、层数、每层的单元数、momentum、mini batch size、regularization perameters等能影响W、b的都称为超参数,超参数的选择需要不断尝试和靠经验,以及一些策略。
深度学习和大脑其实没什么直接关系。
原文:https://www.cnblogs.com/henuliulei/p/11361200.html