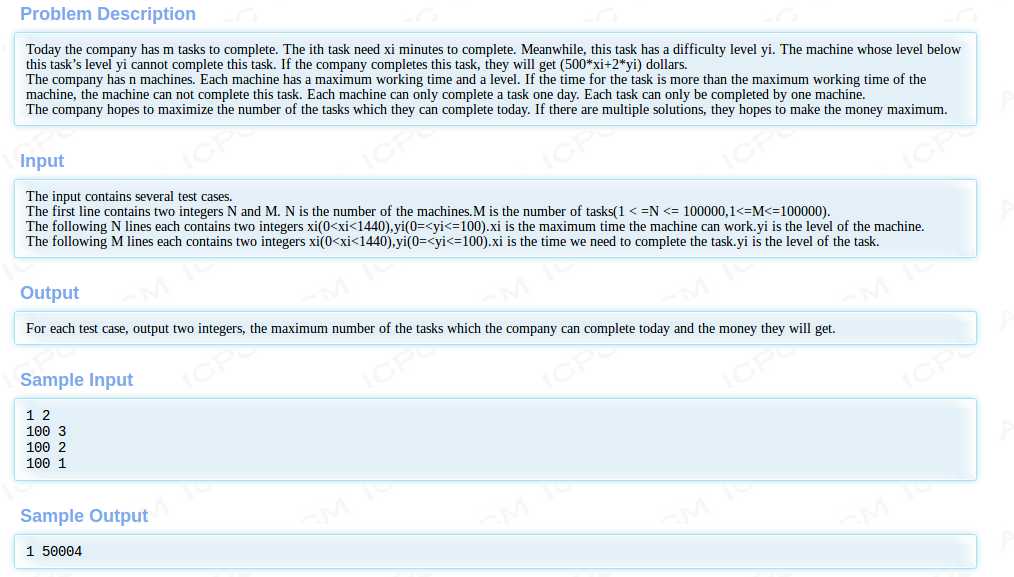
$Description$
$Sol$
$yi<=100$,而收益为$xi*500+yi*2$,说明无论在何种情况下,$xi$较大的产品产生的收益一定大于$xi$较小的产品.随便证下:
$xi=xj+1,yi=0,yj=100$这种极值情况都满足,所以就$OK$辣
所以将按照$xi$为第一关键字,$yi$为第二关键字从大到小排序,对于每一个产品,找到工作时间不小于$xi$并且等级最小的机器完成它.
考虑正确性似乎就只要看这样贪心会不会造成完成的产品数量减少.
不会!假设这里有两个产品$i,j$.分两种情况讨论一下:
1) $xi>xj,yi>yj$
$i$机器可选但没选的机器在时间上肯定能完成$j$,又因为$i$选了等级最小的,所以剩下的在等级上也肯定能完成$j$.如果没有剩下的,说明本来最多就只能完成$i,j$中的一个,那显然选$i$收益更大
2) $xi>xj,yi<yj$ 和上面差不多
$over!$
再讲下实现叭,想完上面的之后,立马就可以想到$O(nm)$大暴力$ovo$,显然过不了.所以我们要维护一个数组,里面存的机器的$x$是大于等于当前任务的$x$的.(套路叭,先排排序,然后按照一定要求向候选集合里面加入元素,再维护些别的).然后发现只要找到最小的$y$就好了.于是就用了一个桶排之类的数组,下标为$y$,值为个数...
讲的很凌乱因为下课了我要出去吃东西了$qwq$.
$Code$

#include<bits/stdc++.h> #define il inline #define Rg register #define go(i,a,b) for(Rg int i=a;i<=b;i++) #define yes(i,a,b) for(Rg int i=a;i>=b;i--) #define mem(a,b) memset(a,b,sizeof(a)) #define ll long long #define db double #define inf 1e7 using namespace std; il int read() { int x=0,y=1;char c=getchar(); while(c<‘0‘||c>‘9‘){if(c==‘-‘)y=-1;c=getchar();} while(c>=‘0‘&&c<=‘9‘){x=(x<<1)+(x<<3)+c-‘0‘;c=getchar();} return x*y; } const int N=100010; int n,m,as1,sum[110];ll as; bool f[N]; struct node{int x,y;}a[N],b[N]; il bool cmp(node x,node y){if(x.x==y.x)return x.y>y.y;return x.x>y.x;} int main() { while(cin>>n>>m) { as=as1=0;mem(sum,0); go(i,1,n)a[i]=(node){read(),read()}; go(i,1,m)b[i]=(node){read(),read()}; sort(a+1,a+n+1,cmp); sort(b+1,b+m+1,cmp); Rg int j=1; go(i,1,m) { while(j<=n && a[j].x>=b[i].x)sum[a[j++].y]++; go(k,b[i].y,100)if(sum[k]){as1++;as+=b[i].x*500+b[i].y*2;sum[k]--;break;} } printf("%d %lld\n",as1,as); } return 0; }
原文:https://www.cnblogs.com/forward777/p/11279538.html