快速幂 笔记与思路整理

鶸就会一种快速幂，以后再写别的吧

当你把一道题公式都推出来了，自以为AC在望的时候看到：

1 ≤ M ≤ 10¹⁰，1 ≤ N ≤ 10¹²，你算出来答案为M^N 对啥啥取模……

朴素的算法（包括pow()函数）就是for循环，一遍一遍a*a*a*a*a……时间复杂度O(n)。对于某些变态数据肯定是不够的，就需要用一些方法加速幂运算。

由于幂运算的性质，aⁿ = aⁿ¹ * aⁿ² ( n1 + n2 = n )。

因此对于ab，利用二进制思想，转化为a^{( 2^t1 *2^t2 * 2^t3 * ... * 2^tn )}

用公式整理一下，

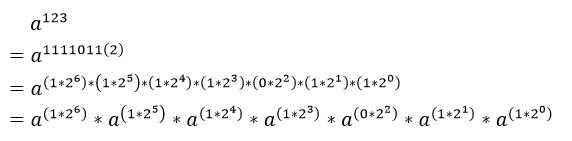
用代码实现出来，只需要运算2*6=12次，时间复杂度O(log n)。

int quick_pow(int a, int b){
    int rslt = 1;
    while(b){
        if(b & 1) rslt *= a;
        a *= a;
        b >>= 1;
    }
    return rslt;
}
///////////////另一种写法///////////////
int quick_pow(int a, int b){
    int rslt = 1;
    for(int i=0; i<20; i++){
        if((1 << i) & b) rslt *= a;
        a *= a;
    }
    return rslt;
}

当然实际运算可能要上long long还有取模啥的。

快速幂 笔记与思路整理

原文：https://www.cnblogs.com/miserweyte/p/11367689.html