当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。通常来说，从两个方面考虑来选择特征：

• 特征是否发散：如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，这个特征对于样本的区分并没有什么用。
• 特征与目标的相关性：这点比较显见，与目标相关性高的特征，应当优选选择。除方差法外，本文介绍的其他方法均从相关性考虑。

根据特征选择的形式又可以将特征选择方法分为3种：

• Filter：过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。
• Wrapper：包装法，根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。
• Embedded：嵌入法，先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。

一、过滤法（filter）

根据特征的相关性进行评分，设定一个评分阈值来选择。

1、方差筛选

方差越大的特征，那么我们可以认为它是比较有用的。如果方差较小，比如小于1，那么这个特征可能对我们的算法作用没有那么大。最极端的，如果某个特征方差为0，即所有的样本该特征的取值都是一样的，那么它对我们的模型训练没有任何作用，可以直接舍弃。

2、相关系数

主要用于输出连续值的监督学习算法中。我们分别计算所有训练集中各个特征与输出值之间的相关系数，设定一个阈值，选择相关系数较大的部分特征。

3、假设检验

卡方检验，是一种以χ²分布为基础的一种常用假设检验方法，它的无效假设H₀是：观察频数与期望频数没有差别。

基本思想：假设H0成立，计算出χ²值，表示观察值与理论值之间的偏离程度，根据χ²分布及自由度可以确定在H₀假设成立的情况下获得当前统计量及更极端情况的概率P。如果P值很小，说明观察值与理论值偏离程度太大，应当拒绝无效假设。

4、互信息

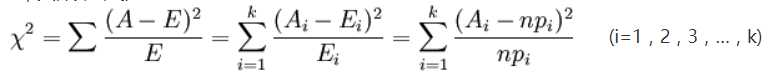
从信息熵的角度分析各个特征和输出值之间的关系评分。互信息值越大，说明该特征和输出值之间的相关性越大，越需要保留。

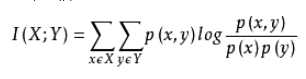
P（x,y）:联合分布

二、包装法（Wrapper）

1、递归消除特征（RFE，recursive feature elimination）

使用一个机器学习模型进行多轮训练，每轮训练后，消除若干权值系数的特征，然后在新的特征集上重新训练，直到满足我们要求的特征数量。

经典的SVM-RFE算法，第一轮训练，选择所有的特征进行训练，以每个特征为正例得到最佳超平面，最后每个特征对应的最佳超平面w的平方值最小的，就排除。然后下一轮训练。

三、嵌入法（Embedded）

1、带惩罚项的特征选择法

使用带惩罚项的基模型，除了筛选出特征外，同时也进行了降维。

L1或L2正则化，正则化惩罚项越大，那么模型的系数就会越小。当正则化惩罚项大到一定的程度的时候，部分特征系数会变成0，当正则化惩罚项继续增大到一定程度时，所有的特征系数都会趋于0. 但是我们会发现一部分特征系数会更容易先变成0，这部分系数就是可以筛掉的。

L1或L2正则化，正则化惩罚项越大，那么模型的系数就会越小。当正则化惩罚项大到一定的程度的时候，部分特征系数会变成0，当正则化惩罚项继续增大到一定程度时，所有的特征系数都会趋于0. 但是我们会发现一部分特征系数会更容易先变成0，这部分系数就是可以筛掉的。

2、基于树模型

可以使用决策树或者GBDT，不是所有的机器学习方法都可以作为嵌入法的基学习器，一般来说，可以得到特征系数coef或者可以得到特征重要度(feature importances)的算法才可以做为嵌入法的基学习器。

3、特征组合（高级特征）

例如：想要知道车子速度，但没有这个特征数据，只有车子的公里数和时间，那么这个高级特征就是由公里数和时间这两个特征计算得到的。

5、特征选择

原文：https://www.cnblogs.com/pacino12134/p/11369021.html