标量(saclar):
就是一个单独的数,没有方向,只具有数值大小,用斜体来表示,被赋予小写的变量名称,比如 斜体小写字母 k 可以表示一条线的斜率,n 可以表示一个集合中元素的数目。
向量(vector):
一个向量是一列数,这些数是有序排列的,通过次序中的索引,我们可以确定每个单独的数,通常用粗体的小写变量名称表示,比如,向量中的元素可以通过带脚标的斜体表示。 向量 x 的第一个元素是 x1,第二个元素是 x2 ,等等。我们也会注明存储在向量中的元素是什么类型的。如果每个元素都属于实数集 R,并且该向量有 n 个元素,那么该向量属 于实数集 R 的 n 次笛卡尔乘积构成的集合,记为 Rn 。当我们需要明确表示向量中的元素时,我们会将元素排列成一个方括号包围的总队:
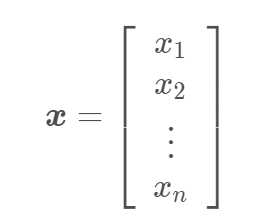
我们可以把向量看作空间重的点,每个元素使不同的坐标轴上的坐标。
有时候我们需要索引向量中的一些元素。在这种情况下,我们定义一个包含这些元素的索引集合,然后将该集合写在脚标处。比如,指定x1,x3和x6,我们定义集合s={1,3,6},然后写 作xs。我们用符 - 表示集合的补集中的索引。 比如x_1 表示x中除了x1以外的所有元素,x_s表示x中除了x1,x3和x6外所有的元素构成的向量。
矩阵(matrix):
矩阵是一个二维数组,其中的每一个元素被两个索引(而非一个)所确定。矩阵通常用粗体的 大写字母表示,比如 A, 如果一个实数矩阵高度为m,宽度为n,那么我们说 A ∈ Rmxn ,
我们在表示矩阵中的元素时。通常以不加粗的斜体形式使其用名称,索引用逗号间隔。比如,
A1,1表示在矩阵A中左上角的那个元素,Am,n表示A右下的元素。我们通过用:表示要用到一排了或 者一列了。比方说Am,:表示我要使用m行所有的元素。
有时我们需要矩阵值表达式的索引,而不是单个元素。在这种情况下,我们在表达式后面接下标, 但不必将矩阵的变量名称小写化。
张量(tensor):
在某些情况下,我们会讨论坐标超过两维的数组。一般地,一个数组中的元素分布在若干维 坐标的规则网格中,我们称之为张量。我们使用字体 A 来表示张量 “A’’。张量 A中坐标为 (i,j,k) 的元素记作 Ai,j,k.
转置(transpose):
矩阵的转置是以对角线为轴的镜像,这条从左上角到右下角的对角线被称为主对角线(main diagonal)。我们将矩阵 A 的转置表示为 AT, 定义如下
(AT)i,j = Ai,j

向量可以看作只有一列的矩阵。对应地,向量的转置可以看作是只有一行的矩阵。有时,我们通过将向量元素作为行矩阵写在文本行中,然后使用转置操作将其变为标准的列向 量,来定义一个向量,比如 x = [x1; x2; x3]?.标量可以看作是只有一个元素的矩阵。因此,标量的转置等于它本身, a = aT。
原文:https://www.cnblogs.com/ccdblogs/p/11368971.html