int add(int a, int b){
return a & b == 0 ? a ^ b : add(a ^ b, (a & b) << 1);
}问题描述:数组中有一个元素出现了p次,其他元素均出现了k次,求该元素
解决方法:
正常思路是统计每个元素出现的次数,即可求出该元素,通过位运算,我们可以实现对元素的统计
先令p = p % k,这样我们统计的上限最多为k,需要\(m = \log \left \lceil k \right \rceil\)个位来表示,也就是对每个位进行计数。
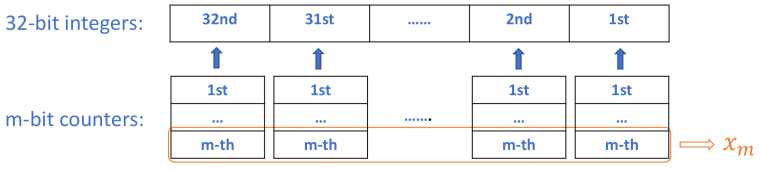
我们先单单看一位,比如32位整数的第一位1st,对于新来的数,如果新来的数该位为1,则我们需要增加第一位对应的m-counter计数器,当计数器达到k时清空为0,最后的p的二进制表示对应的x即可。
先用一个例子说明一下,如k=5,p=3那么对于32位整数的第一位而言,如果single number的该位为1的话,那么该位对应的计数器必定计数了k * r(r为整数) + p次,由于p=3(二进制11)那么该计数器的第一位和第二位都会被置为1,其他位同理,返回x1或者x2即可
现在的主要问题就为当一个位上的1或0来的时候
xm ^= (xm-1 & xm-2 & .. & i)
xm-1 ^= ( xm-2 & .. & i)
x1 ^= i对于第二个问题,我们可以用掩码解决,假定k的二进制表示为101,那么只要第3位和第1位为1,说明计数器已满,需要清0
mask = ~ (x1 & ~x2 & x3)
x1 &= mask
xm &= mask137.?Single Number II
k=3, p = 1
class Solution {
public:
int singleNumber(vector<int>& nums) {
int x2 = 0, x1 = 0, mask;
for(int i : nums){
x2 ^= (x1 & i);
x1 ^= i;
mask = ~(x1 & x2);
x1 &= mask;
x2 &= mask;
}
return x1;
}
};另一种思路也可以使用01来实现三进制,根据真值表写出逻辑表达式
class Solution {
public:
int singleNumber(vector<int>& nums) {
int a = 0, b = 0;
for(int i = 0; i < nums.size(); i++){
int t = (~a&b&nums[i]) | (a&~b&~nums[i]);
b = (~a&b&~nums[i]) | (~a&~b&nums[i]);
a = t;
}
return a | b;
}
};原文:https://www.cnblogs.com/qbits/p/11369631.html