2019白金之星 第一次初赛 第一题 Polynomial

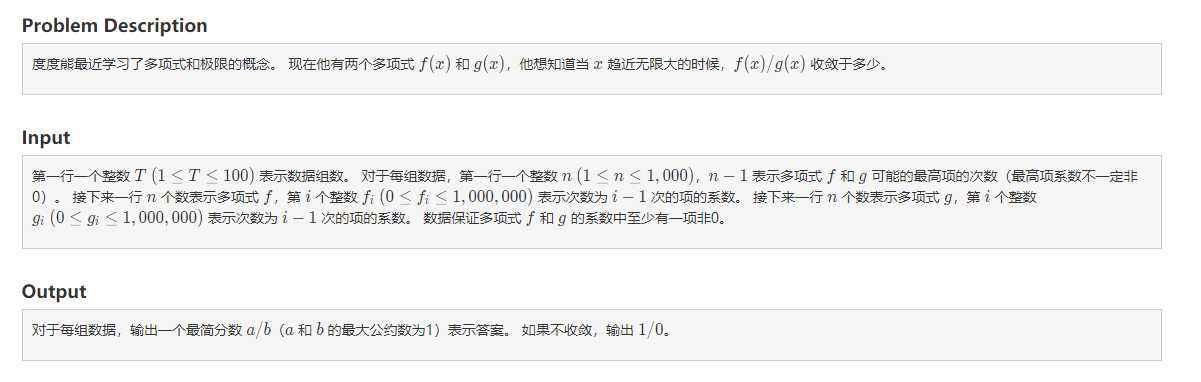
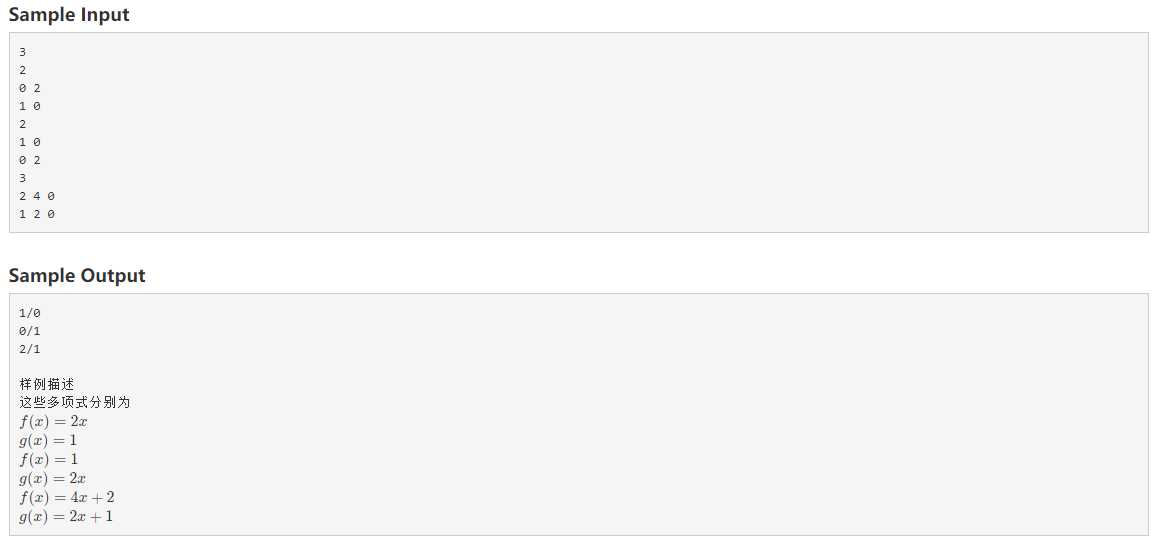
\(\color{blue}{暂时看来我只做了值么一道题(大雾)}\)

思路:

根据导数的知识,(而且只是这种的不带log不带根号的比较好看的函数),每次求导都会使x的每个项降次

当然,每次降次都会把x的0次方项给搞没 .......

所以,我们可以把f(x) 和 g(x) 的x的最高项找出来,最高项次数大的就会存在的时间长,也就是对应的1/0或者0/1 ;

如果f(x)的次数和g(x)的次数相等的话,那就求一个二者的gcd就行啦!

code就放在这里了QAQ

#include <iostream>
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define maxn 1200
#define int long long
using namespace std ;
int T , f[maxn] , f_lop ;
int n , g[maxn] , g_lop ;
signed main() {
    scanf("%d",&T) ;
    while(T --) {
        scanf("%d",&n) ;
        f_lop = g_lop = n-1 ;
        for(int i = 0 ; i < n ; i ++) {
            scanf("%d",&f[i]) ;
        }
        for(int i = 0 ; i < n ; i ++) {
            scanf("%d",&g[i]) ;
        }
        while(!f[f_lop]&&f_lop>0) {
            f_lop --; 
        }
        while(!g[g_lop]&&g_lop>0) {
            g_lop -- ;
        }
        if(f_lop > g_lop) {
            puts("1/0") ;
        }else if(g_lop > f_lop) {
            puts("0/1") ;
        }else {
            int c = __gcd(f[f_lop],g[g_lop]) ;
            cout << f[f_lop]/c << "/" << g[g_lop]/c <<endl ;
        }
    }
    return 0 ;
} 

丑的一批,请多包涵XD

2019白金之星 第一次初赛 第一题 Polynomial

原文：https://www.cnblogs.com/lyt020321/p/11370157.html