Description
国家有一个大工程,要给一个非常大的交通网络里建一些新的通道。
我们这个国家位置非常特殊,可以看成是一个单位边权的树,城市位于顶点上。
在 \(2\) 个国家 \(a,b\) 之间建一条新通道需要的代价为树上 \(a,b\) 的最短路径。
现在国家有很多个计划,每个计划都是这样,我们选中了 \(k\) 个点,然后在它们两两之间 新建 \(C_k^2\) 条 新通道。现在对于每个计划,我们想知道:
这些新通道的代价和;
这些新通道中代价最小的是多少;
这些新通道中代价最大的是多少。
虚树 \(Dp\)。
对于每次的询问,先建出虚树,再进行 \(Dp\)。
建立虚树的关键点:
\(Dp\),其实准确来讲,应该叫做 子树\(Dp\) :
另外 \(ans_1, ans_2, ans_3\) 依次表示答案(距离和,最小值,最大值)。
考虑我们树形 \(Dp\) 在 \(dfs\) 的时候其实是一个不断遇到新的子树的过程,换句话说是一个不断合并两棵子树的过程。于是可以把图画成这样:
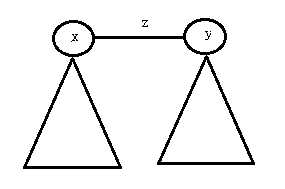
可以先用两棵树的情况更新答案,然后再将 \(y\) 子树的信息合并到 \(x\) 上去,注意必须 \(size[x]>0\)。如果当前 \(x\) 侧还没有任何关键点,就说明此时的 \(f[x],g[x]\) 是没有意义的值,用它们更新答案可能会出错。
最后,在虚树 \(Dp\) 在 \(dfs\) 过程退出的时候要顺手把 \(head\) 清零,如果每次 \(O(n)\) 地清空 \(head\) ,时间是吃不消的。
#include<bits/stdc++.h>
typedef long long ll;
const ll maxn=1e6+10,inf=1e14;
namespace IO
{
char buf[1<<15],*fs,*ft;
inline char getc() { return (ft==fs&&(ft=(fs=buf)+fread(buf,1,1<<15,stdin),ft==fs))?0:*fs++; }
template<typename T>inline void read(T &x)
{
x=0;
T f=1, ch=getchar();
while (!isdigit(ch) && ch^'-') ch=getchar();
if (ch=='-') f=-1, ch=getchar();
while (isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48), ch=getchar();
x*=f;
}
char Out[1<<24],*fe=Out;
inline void flush() { fwrite(Out,1,fe-Out,stdout); fe=Out; }
template<typename T>inline void write(T x,char str)
{
if (!x) *fe++=48;
if (x<0) *fe++='-', x=-x;
T num=0, ch[20];
while (x) ch[++num]=x%10+48, x/=10;
while (num) *fe++=ch[num--];
*fe++=str;
}
}
using IO::read;
using IO::write;
template<typename T>inline bool chkMin(T &x,const T &y) { return x>y ? (x=y, true) : false; }
template<typename T>inline bool chkMax(T &x,const T &y) { return x<y ? (x=y, true) : false; }
struct Graph
{
int ver[maxn<<1],Next[maxn<<1],head[maxn],len;
inline void add(int x,int y)
{
ver[++len]=y,Next[len]=head[x],head[x]=len;
ver[++len]=x,Next[len]=head[y],head[y]=len;
}
}A, T;
ll ans1,ans2,ans3;
namespace Virtual
{
int dfn[maxn],id,dep[maxn],fa[maxn][21];
inline void dfs1(int x)
{
dfn[x]=++id;
for (int i=1; i<=20; ++i) fa[x][i]=fa[fa[x][i-1]][i-1];
for (int i=A.head[x]; i; i=A.Next[i])
{
int y=A.ver[i];
if (y==fa[x][0]) continue;
fa[y][0]=x;
dep[y]=dep[x]+1;
dfs1(y);
}
}
inline int LCA(int x,int y)
{
if (dep[x]>dep[y]) std::swap(x,y);
for (int i=20; i>=0; --i)
if (dep[y]-(1<<i)>=dep[x]) y=fa[y][i];//
if (x==y) return x;
for (int i=20; i>=0; --i)
if (fa[x][i]^fa[y][i]) x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
inline bool cmp(int a,int b)
{
return dfn[a]<dfn[b];
}
int Stack[maxn],top;
bool key[maxn];
inline void insert(int x)
{
if (!top) { Stack[++top]=x; return ; }
int lca=LCA(Stack[top],x);
while (dep[Stack[top-1]]>dep[lca] && top>1)
{
T.add(Stack[top-1],Stack[top]), --top;
}
if (dep[lca]<dep[Stack[top]])
{
T.add(lca,Stack[top]), --top;
}
if (!top || dep[Stack[top]]<dep[lca]) Stack[++top]=lca;
Stack[++top]=x;
}
inline void build(int *c,int k)
{
std::sort(c+1,c+k+1,cmp);
T.len=0;
if (c[1]^1) Stack[top=1]=1;
else Stack[top=0]=0;
for (int i=1; i<=k; ++i) insert(c[i]),key[c[i]]=1;
while (top>1) T.add(Stack[top],Stack[top-1]),--top;
}
typedef ll array[maxn];
array d,f,g,siz;
inline void dfs2(int x,int fa)
{
siz[x]=key[x], d[x]=g[x]=0, f[x]=key[x] ? 0 : inf;
for (int i=T.head[x]; i ; i=T.Next[i])
{
int y=T.ver[i], z=dep[y]-dep[x];
if (y==fa) continue;
dfs2(y,x);
if (siz[x]>0)//siz[x]表示以 x 为根的子树中关键点的数量
{
ans1+=siz[x]*siz[y]*z+siz[y]*d[x]+siz[x]*d[y];
chkMin(ans2,f[x]+z+f[y]);
chkMax(ans3,g[x]+z+g[y]);
}
d[x]+=d[y]+siz[y]*z;//d[x]表示以 x 为根的子树中,各关键点到 x 的距离之和
chkMin(f[x],z+f[y]);//f[x]表示以 x 为根的子树中,关键点到 x 的距离最小值
chkMax(g[x],z+g[y]);//g[x]表示以 x 为根的子树中,关键点到 x 的距离最大值
siz[x]+=siz[y];
}
T.head[x]=key[x]=0;
}
}
using Virtual::dfs1;
using Virtual::build;
using Virtual::dfs2;
int main()
{
int n;read(n);
A.len=T.len=0;
for (int i=1,x,y; i<n; ++i) read(x),read(y),A.add(x,y);
dfs1(1);
int q;read(q);
while (q--)
{
int k;read(k);
int *c=new int[k+10];
for (int i=1; i<=k; ++i) read(c[i]);
build(c,k);
ans1=0, ans2=inf, ans3=0;
dfs2(1,0);
write(ans1,' '), write(ans2,' '),write(ans3,'\n');
delete[] c;
}
IO::flush();
return 0;
}原文:https://www.cnblogs.com/G-hsm/p/11380517.html