·听了一天的浑浑噩噩
·这个老师近距离看有点精致可爱,然鹅他过于强
·老师经典语句:
“来我们看一道简单题”,然鹅,是蓝题
“来我们再来看一道题",然鹅,是紫题
tql!!!tjl!!!%%%%%
一、图的入门介绍
·什么是图?——G(graph)=(V(点),E(边))
把图进行赋值,所赋值即为权值——点权,边权.
·图的储存
edge:next,to.
eg:x——>y
next:下一个以x为开头的边在数组的位置
to:y
first:以x为开头的第一条边
储存方法:找到最后,在往前倒
板子:
struct edge {
int next, to;
edge() {}
edge(int _next, int _to) : next(_next), to(_to) {}
} e[M];
void add_edge(int x, int y) {
e[++tot] = edge(first[x], y);
first[x] = tot;
e[++tot] = edge(first[y], x);
first[y] = tot;
}
int main() {
for (int x = first[p]; x; x = e[x].next) { //find linkers of point p
q = e[x].to;
}
}
升级版板子(带stl):
#include <vector>
vector<int> to[N];
to[x].push_back(y);
for (int x = 0; x < to[p].size(); ++x) {
q = to[p][x]
}
·例题:
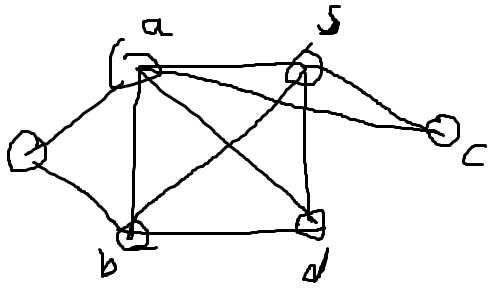
联合权值https://www.luogu.org/problem/P1351
以下为此题温馨提示(dl可自行忽略):
(x,y), dis[x][y]=2.
以s为中心对答案的贡献:
ab+bc+ca+cd+bd+cd
=[(a+b+c+d)²-(a²+b²+c²+d²)]/2.
·相关补充内容:
1、团(完全图)
有n个点,点之间两两都有边,共有n(n-1)/2条边.
【例题:
给定3n个点,保证有一个大小为2n的团.
求任意一个大小为n的团.
——方法:
3n-2n=n.故最多有n个不在团中的点—故删除2n个包括n个不在团中的点即可。
每次找到一个没有连边的点对(x, y),把他们两个都删了.
删n次剩下的就是一个大小为n的团.】
2、图的退化—>树
图:n个点,m条边
树:n个点,n-1条边,连通
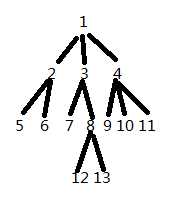
3、dfs序:
顾名思义,dfs序就是dfs的顺序,分两种。
第一种:处理子树问题.
即为 1,2,5,6,3,7,8,12,13,4,9,10,11
第一种dfs序中每个子树可以看成dfs序中的一段连续区间.
子树问题 ? 序列问题
第二种:处理树链问题.
即为 1,2,5,-5,6,-6,-2,3,7,-7,8,12,-12,13,-13,-8,-3,4,9,-9,10,-10,11,-11,-4,-1。
求[1,2,5,4,11]—合并[1,2,5,-5,6,-6,-2,3,7,-7,8,12,-12,13,-13,-8,-3,4,9,-9,10,-10,11]得到[1,4,11]
合并 [1,2,5],由此得到[1,2,5,4,11].
第二种dfs序中每个树链可以看成dfs序中的一段连续区间.
树链问题 ? 序列问题.
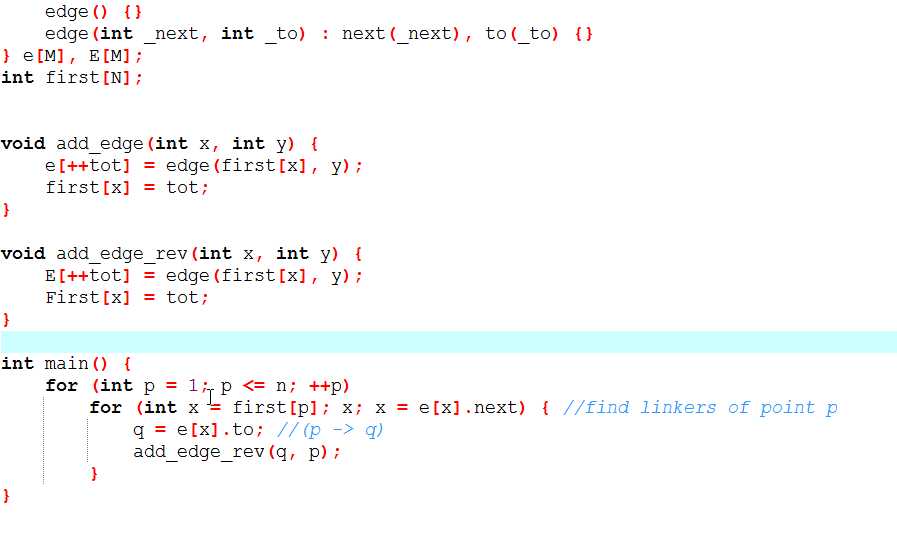
4、取反图
·遍历所有头节点,方向取反.
·直接上板子:
二、最短路
·源点s:起点,汇点T:终点.
·1、单源最短路:一个点为起点,所有点为终点.
2、多源最短路:所有点为起点,所有点为终点.
·求最短路算法:
1、多源:Bellmen Ford (spfa), Floyd
2、单源:Dijkstra
三、flyod
·这是最简单的一个!!!!!!!!!!!
·多源最短路,所有点到所有点。
·动态规划.
·F[i][j][k]表示从i到j的最短路,其中经过的点只有1, 2, 3, …, k, i, j这些.
F[i][j][k] = min(F[i][j][k – 1], F[i][k][k – 1] + F[k][j][k – 1]).
显然k这一维可以省略.
F[i][j] = min(F[i][j], F[i][k] + F[k][j]).
k从1到n遍历一遍就好了.
时间复杂度:O(N^3).
·初始值:没给的边赋值为∞
·板子:
void floyd() {
for (int k = 1; k <= n; ++k)
for (int i = 1; i <= n; ++i)
for (int j = 1; j <= n; ++j)
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
四、dijkstra
·单源最短路,一到多.
·数组dis[],dis[p]表示源点S到点i的最短路径长度.(暂时)
集合T,p∈T表示源点S到点p的最短路径长度已经被求出来了.
·初始化:一开始只有S在T中,除了dis[S] = 0,别的dis = inf.
·贪心思想:每次找到不在T中的所有点中,dis最小的点p,把p丢进T,然后更新所有和p相邻的dis值.
重复n - 1遍上述操作,就求出了n个所有点的最短路.
·考虑先后更新的两个点v1, v2.
由dijkstra的步骤知道,dis[v1] < dis[v2].
而S到v2的前一步,一定经过一个小于dis[v2]的点v.
我们知道这所有的v都已经在v2前已经求出来了,所以的确可以求出来正确的dis[v2].
证明也同时说明,dijkstra算法要求所有的边边权都是正的.
时间复杂度:O(n^2).
堆优化T ? O(nlogn).
·限制条件:所有边的边权为正.
·板子:
struct edges {
int next, to, v;
edges() {}
edges(int _n, int _t, int _v) : next(_n), to(_t), v(_v) {}
} e[];
struct heap_node {
int v, to;
heap_node() {}
heap_node(int _v, int _to) : v(_v), to(_to) {}
};
inline bool operator < (const heap_node &a, const heap_node &b) {
return a.v > b.v; //这里实现的是小根堆,如果要大根堆,把 > 改成 < 即可
}
priority_queue <heap_node> h;
inline void add_to_heap(const int p) {
for (int x = first[p]; x; x = e[x].next)
if (dis[e[x].to] == -1)
h.push(heap_node(e[x].v + dis[p], e[x].to));
}
void Dijkstra(int S) {
memset(dis, -1, sizeof(dis));
while (!h.empty()) h.pop();
dis[S] = 0, add_to_heap(S);
int p;
while (!h.empty()) {
if (dis[h.top().to] != -1) {
h.pop();
continue;
}
p = h.top().to;
dis[p] = h.top().v;
h.pop();
add_to_heap(p);
}
}
五、Bellman Ford(spfa)
·spfa = 队列优化bellman ford.
·初始化:一开始dis[S] = 0, 对于其他的p,dis[p] = inf.
维护一个队列,队列里面存是dis被更新的点.
·每次取出队首,用队首的dis信息更新和它相连的其他点的dis,然后把这些点不在队列里且dis值变小的重新入队.
队列为空表示没有要更新的点,算法结束.
·每次进队列的点都是dis值更新的点.
所以这个点的dis已经最小的话,就不会更新,也就是不会再进队了.
同时这个点的dis能达到最小值,否则它的最短路径上的前一个点的dis也不是最小值,以此类推,所有最小值路径上的dis都不是最小值,也即dis[S] > 0,这显然不对.
·理论复杂度O(NM).
·N是点数,M是边数.
·实际跑起来很快,但是会被特定结构的图卡到理论上界.
e.g. 奶牛题专卡spfa.
一般建议不写.
·SLF优化:
spfa有时候会被卡,这时候适当地添加SLF优化可以不被卡.
SLF优化在特定图下还是会被卡,不过被卡的几率很小.
SLF优化的地方就是每次更新dis进队时,判断一下是不是当前点的dis值比队头还小:如果是的话,直接把当前点插入队头.
只需要加一句if就可以了,很方便而且不容易被卡.
·板子:
纯spfa:
struct edge {
int next, to, v;
}e[];
void spfa(int S) {
int p, x, y, l, r;
for (x = 1; x <= n; ++x)
dis[x] = inf;
q[0] = S, dis[S] = 0, v[S] = 1;
for (l = r = 0; l != (r + 1) % N; ) {
p = q[l], ++l %= N;
for (x = first[p]; x; x = e[x].next)
if (dis[p] + e[x].v < dis[(y = e[x].to)]) {
dis[y] = dis[p] + e[x].v;
if (!v[y]) {
v[y] = 1;
q[++r %= N] = y;
}
}
v[p] = 0;
}
}
带slf优化的spfa:
struct edge {
int next, to, v;
}e[];
int inc(int x) {
x = x + 1;
x = x % N;
return x;
}
int dec(int x) {
x = x - 1 + N;
x = x % N;
return x;
}
void spfa(int S) {
int p, x, y, l, r;
for (x = 1; x <= n; ++x)
dis[x] = inf;
q[0] = S, dis[S] = 0, v[S] = 1;
for (l = r = 0; l != (r + 1) % N; ) {
p = q[l], inc(l);
for (x = first[p]; x; x = e[x].next)
if (dis[p] + e[x].v < dis[(y = e[x].to)]) {
dis[y] = dis[p] + e[x].v;
if (!v[y]) {
v[y] = 1;
if (dis[y] < dis[q[l]]) q[dec(l)] = y; //SLF
else q[inc(r)] = y;
}
}
v[p] = 0;
}
}
·TIPS:求最短路可用bfs,不要用dfs(否则会爆时)
·相关补充内容:
出边:出去;入边:进入。
出度:往外指的边的条数;入度:指向它的边的条数。
六、差分约束系统
·一组二元不等式.
·题面:
x[i] – x[j] ≤ k.
求x[i] – x[0]的最小值.
·对一个x[i] – x[j] ≤ k:
j指向i有一条长度为k的边.
求以0为起点的最短路.
·对照:

·什么时候无解?
---有负环的时候.
eg:x[2]-x[1]<=-1
x[1]-x[2]<=-1
相加,0<=-2,显然不成立,故无解.
·如果把小于号改成大于号,求最小值呢?
---最长路.
·如果有一部分是大于号并且求最大值呢?
---把大于号改成小于号并求最短路.
七、二分图匹配
·二分图:两部分:一部分点集为x、y,x、y中两两不相连.
·匹配:左边点与右边点连成一条边。
二分图匹配:能连多少边且每个点至多被连了一次。
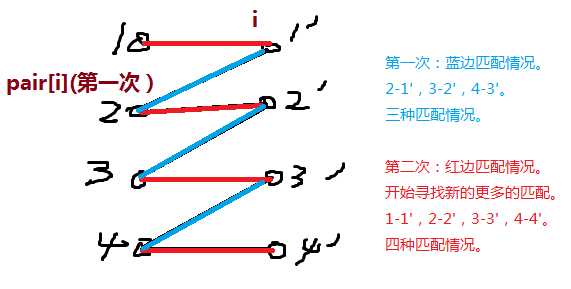
·算法:匈牙利算法:介于当前匹配情况去搜有没有更大的匹配,找到一个之前未匹配的点.
找到2个点,2/2=1,3—>4。
每次加新边,右边只能dfs一次.
贪心的思想.
每次找一条路径,是非匹配-匹配相互交替的.
如果找到一个2k长度的路径,说明有一个更大的匹配方式.
每次找路径都是暴力搜,所以每次寻找路径都要搜满m条边.
对每个点都要搜一次,所以总时间复杂度是O(NM).
·板子:
int find(int x) {
for (int i = 1; i <= n; ++i)
if (a[x][i] == 1 && flag[i] == 0) {
flag[i] = 1;
if (pair[i] == 0 || find(pair[i])) {
pair[i] = x;
return 1;
}
}
return 0;
}
int edmonds() {
int cnt = 0;
memset(pair, 0, sizeof(pair));
for (int i = 1; i <= n; ++i) {
memset(flag, 0, sizeof(flag));
if (find(i)) ++cnt;
}
return cnt;
}
八、Kruskal,最小生成树
·生成树:(对不起我也解释不好请自行意会)就是在原树上生成的一棵小树.
·最小生成树:边权最小的生成树.
·一般在无向图上做.
·最小生成树的性质:对于一条不在最小生成树上的边,它与最小生成树形成了一个环,那么这个环上这条边的权值是最大的之一.
做题基本要用到这个大佬的性质.
· 最小生成树不是唯一的,往往存在多个。
·算法:Kruskal
把所有边权从小到大排序,依次检查每一条边是否在最小生成树上.
两种case:
1. 边两边的点本来已经在同一棵树中了,那么会形成一个环.
2. 边两边的点不来不在一棵树中,那么会把两棵树变成一棵.
对于case1,显然环上其他的边权值都不大于它,也就是说它是环上权值最大的边之一,故它不应该在最小生成树上.
对于case2,直接把这条边加入最小生成树就可以了.
·怎么判断两个点在不在同一棵树里?
并查集!
一开始每个点都在一个独立的集合里.
每次合并两棵树 ? 集合并.
查询插入边有没有成环 ? 集合查询.
并查集作用:检查连通性。
两点不连通—>加边。
两点原来连通—>不加边。
把所有点都加一遍。
·最小生成树:从小往大加边。
最大生成树:从大往小加边。
·板子:
struct edges{
int from, to, v;
edges() {}
edges(int a, int b, int c) : from(a), to(b), v(c) {}
}e[];
inline bool operator <(const edges &a, const edges &b){
return a.v < b.v; //如果是最大生成树,则把 < 改成 > 即可
}
inline void add_edge(int X, int Y, int Z){
e[++tot] = edges(X, Y, Z);
}
int find_fa(int x){
return x == fa[x] ? x : fa[x] = find_fa(fa[x]);
}
int Kruskal(){
sort(e + 1, e + tot + 1);
int i;
for (i = 1; i <= n; ++i)
fa[i] = i;
int fax, fay, cnt = n - 1, res = 0;
for (i = 1; i <= tot; ++i){
fax = find_fa(e[i].from), fay = find_fa(e[i].to);
if (fax != fay){
--cnt;
fa[fax] = fay;
res += e[i].v;
if (!cnt) return res;
}
}
return -1;
}
·相关补充内容:
次大生成树。
例题:Bzoj1977次小生成树Tree
-严格次小生成树:当前次小生成树边权和>最小生成树边权和.
改一条边。
-做法:最小生成树+LCA
先做出一个MST.
对每一条非树边边,加入MST后会形成一个环.
删除环上的除了这条非树边的最大值就好了.
但是权值可能相同,所以还要记录一下严格次大边是多少.
-板子:
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 100001;
const int M = 300001;
struct data{
int x, y, v;
bool selected;
}a[M];
struct edge{
int next, to ,v;
}e[N * 2];
struct tree_node{
int dep, fa[17], d1[17], d2[17];
}tr[N];
inline bool operator < (const data a, const data b){
return a.v < b.v;
}
int n, m, cnt, tot, del = 1e9;
int first[N], fa[N];
ll ans;
inline int read(){
int x = 0, sgn = 1;
char ch = getchar();
while (ch < ‘0‘ || ch > ‘9‘){
if (ch == ‘-‘) sgn = -1;
ch = getchar();
}
while (ch >= ‘0‘ && ch <= ‘9‘){
x = x * 10 + ch - ‘0‘;
ch = getchar();
}
return sgn * x;
}
inline void add_edge(int x, int y, int z){
e[++tot].next = first[x], first[x] = tot;
e[tot].to = y, e[tot].v = z;
}
void add_Edges(int X, int Y, int Z){
add_edge(X, Y, Z);
add_edge(Y, X, Z);
}
int find_fa(int x){
return x == fa[x] ? x : fa[x] = find_fa(fa[x]);
}
void dfs(int p){
int i, x, y, FA;
for (i = 1; i <= 16; ++i){
if (tr[p].dep < (1 << i)) break;
FA = tr[p].fa[i - 1];
tr[p].fa[i] = tr[FA].fa[i - 1];
tr[p].d1[i] = max(tr[p].d1[i - 1], tr[FA].d1[i - 1]);
if (tr[p].d1[i - 1] == tr[FA].d1[i - 1])
tr[p].d2[i] = max(tr[p].d2[i - 1], tr[FA].d2[i - 1]);
else {
tr[p].d2[i] = min(tr[p].d1[i - 1], tr[FA].d1[i - 1]);
tr[p].d2[i] = max(tr[p].d2[i - 1], tr[p].d2[i]);
tr[p].d2[i] = max(tr[p].d2[i], tr[FA].d2[i - 1]);
}
}
for (x = first[p]; x; x = e[x].next)
if ((y = e[x].to) != tr[p].fa[0]){
tr[y].fa[0] = p, tr[y].d1[0] = e[x].v, tr[y].dep = tr[p].dep + 1;
dfs(y);
}
}
inline int lca(int x, int y){
if (tr[x].dep < tr[y].dep) swap(x, y);
int tmp = tr[x].dep - tr[y].dep, i;
for (i = 0; i <= 16; ++i)
if ((1 << i) & tmp) x = tr[x].fa[i];
for (i = 16; i >= 0; --i)
if (tr[x].fa[i] != tr[y].fa[i])
x = tr[x].fa[i], y = tr[y].fa[i];
return x == y ? x : tr[x].fa[0];
}
void calc(int x, int f, int v){
int mx1 = 0, mx2 = 0, tmp = tr[x].dep - tr[f].dep, i;
for (i = 0; i <= 16; ++i)
if ((1 << i) & tmp){
if (tr[x].d1[i] > mx1)
mx2 = mx1, mx1 = tr[x].d1[i];
mx2 = max(mx2, tr[x].d2[i]);
x = tr[x].fa[i];
}
del = min(del, mx1 == v ? v - mx2 : v - mx1);
}
void work(int t, int v){
int x = a[t].x, y = a[t].y, f = lca(x, y);
calc(x, f, v);
calc(y, f, v);
}
int main(){
n = read(), m = read();
int i, f1, f2, TOT = 0;
for (i = 1; i <= m; ++i)
a[i].x = read(), a[i].y = read(), a[i].v = read();
for (i = 1; i <= n; ++i)
fa[i] = i;
sort(a + 1, a + m + 1);
for (i = 1; i <= m; ++i)
if ((f1 = find_fa(a[i].x)) != (f2 = find_fa(a[i].y))){
fa[f1] = f2;
ans += a[i].v;
a[i].selected = 1;
add_Edges(a[i].x, a[i].y, a[i].v);
++TOT;
if (TOT == n - 1) break;
}
dfs(1);
for (i = 1; i <= m; ++i)
if (!a[i].selected)
work(i, a[i].v);
printf("%lld\n", ans + del);
return 0;
}
Ps/ h[][]记录严格次大边,G[][]记录最大边
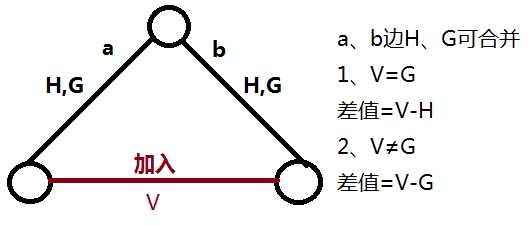
在处理时,如上述代码,a、b边可分开处理。
原文:https://www.cnblogs.com/konglingyi/p/11384786.html