
1 #include<iostream> 2 #include<cstdio> 3 #include<cmath> 4 #include<string> 5 #include<cstring> 6 #include<algorithm> 7 using namespace std; 8 namespace Moxing { 9 const int mod=1000000000; 10 int n,m,cnt,k[95][95];int a[95][95],d[95][95],idx[11][11]; 11 char s[11][11]; 12 bool check(int x,int y) { 13 return (x>=1)&&(x<=n)&&(y>=1)&&(y<=m)&&(s[x][y]==‘.‘); 14 } 15 long long gauss() { 16 long long ans=1; 17 for(int j=1;j<=cnt;j++){ 18 for(int i=j+1;i<=cnt;i++){ 19 while(k[i][j]){ 20 long long t=k[j][j]/k[i][j]; 21 for(int g=j;g<=cnt;g++){ 22 k[j][g]=(k[j][g]-t*k[i][g]%mod+mod)%mod; 23 swap(k[i][g],k[j][g]); 24 }//puts("Moxing"); 25 ans*=-1; 26 } 27 } 28 ans=ans*k[j][j]%mod; 29 } 30 return (ans+mod)%mod; 31 } 32 struct main { 33 main() { 34 35 scanf("%d%d",&n,&m); 36 for(int i=1; i<=n; i++) { 37 scanf("%s",s[i]+1); 38 for(int j=1;j<=m;j++){ 39 if(s[i][j]==‘.‘){ 40 idx[i][j]=++cnt; 41 } 42 } 43 } 44 for(int i=1; i<=n; i++) { 45 for(int j=1; j<=m; j++) { 46 if(!check(i,j)) continue ; 47 if(check(i+1,j)) { 48 d[idx[i][j]][idx[i][j]]++; 49 d[idx[i+1][j]][idx[i+1][j]]++; 50 a[idx[i][j]][idx[i+1][j]]=a[idx[i+1][j]][idx[i][j]]=1; 51 } 52 if(check(i,j+1)) { 53 d[idx[i][j]][idx[i][j]]++; 54 d[idx[i][j+1]][idx[i][j+1]]++; 55 a[idx[i][j]][idx[i][j+1]]=a[idx[i][j+1]][idx[i][j]]=1; 56 } 57 } 58 } 59 cnt--; 60 for(int i=1; i<=cnt; i++) { 61 for(int j=1; j<=cnt; j++) { 62 k[i][j]=((d[i][j]-a[i][j])+mod)%mod;//,cout<<k[i][j]<<‘ ‘; 63 } 64 } 65 printf("%lld\n",gauss()); 66 exit(0); 67 } 68 } UniversalLove; 69 } 70 int main() { 71 Moxing::main(); 72 }
以下内容部分参考https://www.cnblogs.com/zj75211/p/8039443.html。
对于一个无向图 G ,它的生成树个数等于其基尔霍夫Kirchhoff矩阵任何一个N-1阶主子式的行列式的绝对值。
所谓的N-1阶主子式就是对于一个任意的一个 r ,将矩阵的第 r 行和第 r 列同时删去得到的新矩阵。
基尔霍夫矩阵的一种求法:K =度数矩阵 D - 邻接矩阵 A
具体构造
度数矩阵D:是一个 N×NN×N 的矩阵,其中D[i][j]=0(i≠j)D[i][j]=0(i≠j),D[i][i]=i号点的度数D[i][i]=i号点的度数
邻接矩阵A:是一个 N×NN×N 的矩阵,其中A[i][i]=0,A[i][j]=A[j][i]=i,j之间的边数A[i][i]=0,A[i][j]=A[j][i]=i,j之间的边数
基尔霍夫矩阵K=D-A
行列式求法
行列式在数学中是一个函数。其定义域为det的矩阵A,取值为一个标量,写作det(A)或|A|。
对于一个n*n的矩阵A,我们枚举n个数的所有排列p,定义其逆序对数为r(p)。
则有|A|=∑p(-1)^r(p)∏(i=1 to n)ai,pi。求和式的每一项可以看做是在矩阵中选出N个数,使得他们的行列都不重合。
高斯消元把矩阵消成一个上三角,主对角线上的元素乘积即为答案。
记得记录交换两行的次数,次数为奇数则为负。
如果主对角线上有0,则说明原矩阵中存在两行线性相关,故行列式也应该为0;
图示上三角矩阵:
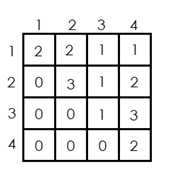
行列式其他性质
性质1 互换矩阵的两行(列),行列式变号。
性质2 如果矩阵有两行(列)完全相同,则行列式为 0
性质3 如果矩阵的某一行(列)中的所有元素都乘以同一个数k,新行列式的值等于原行列式的值乘上数k。
推论:如果矩阵的某一行(列)中的所有元素都有一个公因子k,则可以把这个公因子k提到行列式求和式的外面。
性质3 如果矩阵有两行(列)成比例(比例系数k),则行列式的值为 0
性质4 如果把矩阵的某一行(列)加上另一行(列)的k倍,则行列式的值不变。
bzoj4031: [HEOI2015]小Z的房间-Matrix Tree/行列式
原文:https://www.cnblogs.com/Moxingtianxia/p/11385515.html