Splay作为平衡树家族中最著名的一员,又可以作为LCT的辅助树 ——
这就是我先学它以及本文讲解它的理由(小声)
它能作为Link Cut Tree的辅助树是因为Splay可以进行独特的区间翻转,其他树 我不知道, 大概是不能。
这个玩意又是Tarjan发明的。 (%%%Tarjan)
这篇题解会涉及一些其它题解没有的玩意儿,来帮助读者更好的理解Splay的实现。
不知道什么是平衡树的自行度娘。
Splay的核心思想
就是通过不断的改变树的形态来保证树不会(一直)是一条链,从而保证复杂度。
在以下代码中:
struct TREE{ int f,val,w,siz;
//该节点的父亲, 值, 相同值的个数(有时候为1,可去掉这个域), 子树大小(就是包括自己,下面有几个节点) int ch[2];
//0:左儿子 1:右儿子 (方便利用表达式进行操作) }t[N],_NULL;
//树 和一个空白 int root,tot;
//根节点的序号 节点个数 queue<int>rec;
//回收节点的队列 #define LS (t[u].ch[0]) #define RS (t[u].ch[1])
首先是单旋rotate ,使得X向上一位。先上代码。
void push_up(int u){ //get t[u].siz t[u].siz=t[u].w+t[LS].siz+t[RS].siz; } void Connect(int son,int fa,int rel){ //son father & relation t[fa].ch[rel]=son; t[son].f=fa; } void rotate(int X){ //let X be his grandparent‘s son int Y=t[X].f,Z=t[Y].f; int B=t[X].ch[t[Y].ch[0]==X], X_pos=t[Y].ch[1]==X; int Y_pos=t[Z].ch[1]==Y; Connect(B,Y,X_pos); Connect(Y,X,X_pos^1); //?!X_pos Connect(X,Z,Y_pos); push_up(Y); push_up(X); }
上几张图来讲解一下,尤其是那几个奇怪的Connect。
首先单旋的过程是这样的:显然大小关系不变
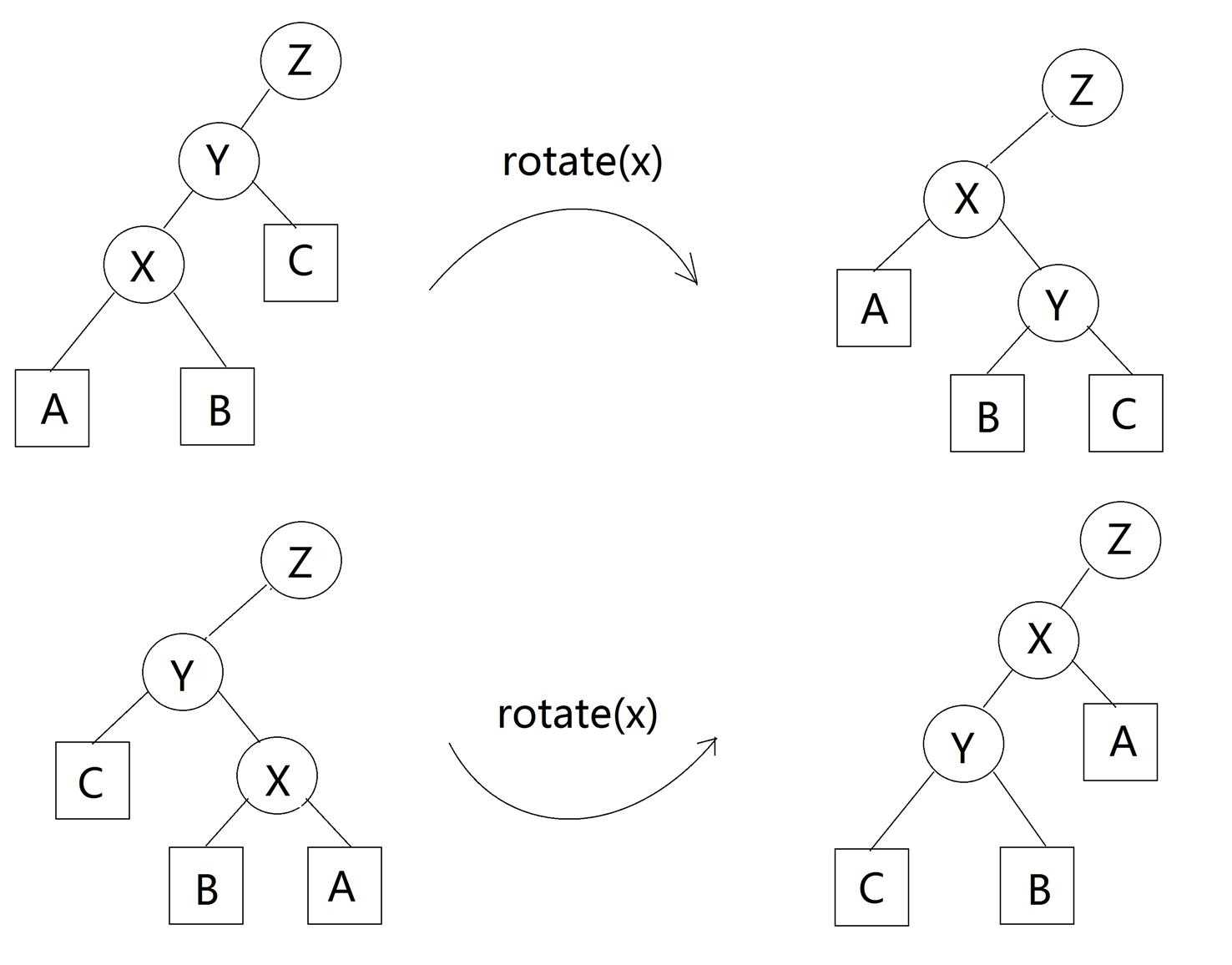
原文:https://www.cnblogs.com/lsy263/p/11390614.html