偏差与方差

偏差与方差的权衡

• 复杂的假设集
  • 较好的近似,较差的泛化
  • 获得更好的接近目标函数的机会,但寻找最优假设式是个问题
• 简单的假设集
  • 较好的泛化,较差的近似
  • 容易找到最优假设式,但近似效果可能很差

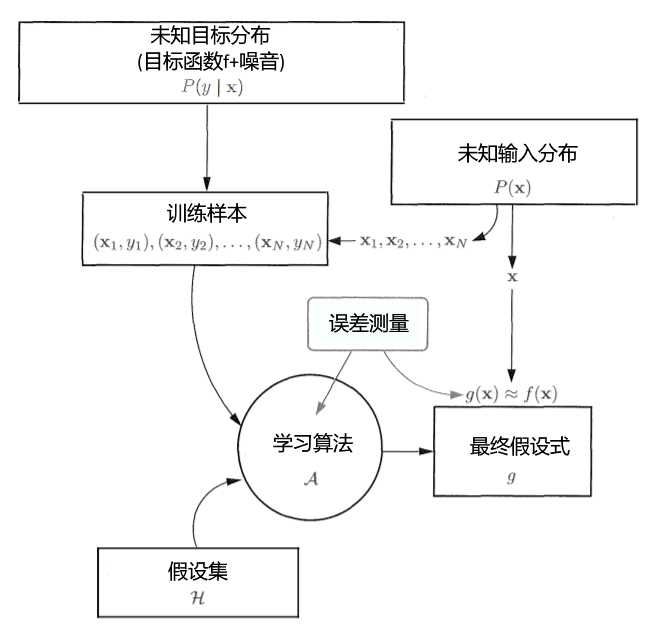
偏差与方差分析可以是另一个问题,将E\(_{out}\)分解为:

1. 假设集H可以多好地近似目标函数f
2. 你可以多好地从假设集中确定一个优的h

从Eout推导偏差与方差

以下分析作用于二元的回归问题,误差测量使用平方误差,假设有数据集\(D_1,D_2,...,D_n\)

\(g^{(D)}\)是指作用于特定的数据集得到的最终假设式(这也意味着不同的数据集可能得到不同的最终假设式)

\(E_x[...]\)是指取作用于所有样本点x的期望(也就是平均值)

\(E_D[...]\)是指取作用于所有数据集D的期望(也就是平均值)

\(\overline{g}(x)=E_D[g_{(D)}(x)]\)是指是指取作用于所有数据集D得到的最终假设式的期望(也就是平均值)

• 作用于特定数据集下的误差

\(E_{out}(g^{(D)})=E_x[(g^{(D)}(x)-f(x))^2]\)

• 作用于所有数据集下的误差

\(E_D[E_{out}(g^{(D)})]=E_D[E_x[(g^{(D)}(x)-f(x))^2]]\)

? \(=E_x[E_D[(g^{(D)}(x)-f(x))^2]]\)

? \(=E_x[E_D[(g^{(D)}(x)-\overline{g}(x)+\overline{g}(x)-f(x))^2]]\)

? \(=E_x[E_D[(g^{(D)}(x)-\overline{g}(x))^2+(\overline{g}(x)-f(x))^2+2(g^{(D)}(x)-\overline{g}(x))(\overline{g}(x)-f(x))]]\)

\(\overline{g}(x)=E_D[g_{(D)}(x)]\)和f(x)与作用在不同的数据集无关,所以\(E_D(\overline{g}(x)-f(x))\)可以视作一个常数,\(E_D(g^{(D)}(x)-\overline{g}(x))\)明显为零

? \(=E_x[E_D[(g^{(D)}(x)-\overline{g}(x))^2]+(\overline{g}(x)-f(x))^2]\)

? \(=E_x[方差(x)+偏差(x)]\)

? \(=方差+偏差\)

直观认识

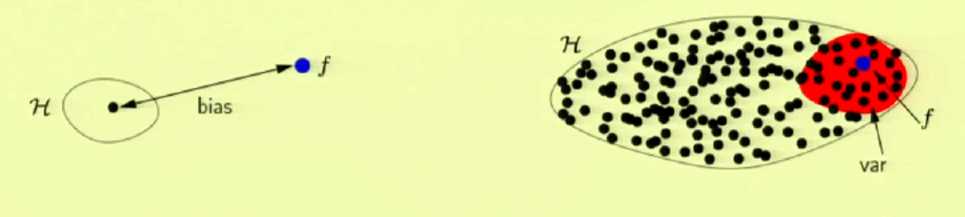
黑点代表一个假设式,蓝点代表目标函数,红色区域代表方差

从一个简单的假设集到一个复杂的假设集,偏差减小,方差增大(更好的近似,更弱的泛化)

• 偏差指的是假设集中的最优假设式接近目标函数f的程度(假设集H可以多好地近似目标函数f)
• 方差是指作用于不同数据集得到的最终假设式接近最优假设式的程度(你可以多好地从假设集中确定一个优的h)

案例

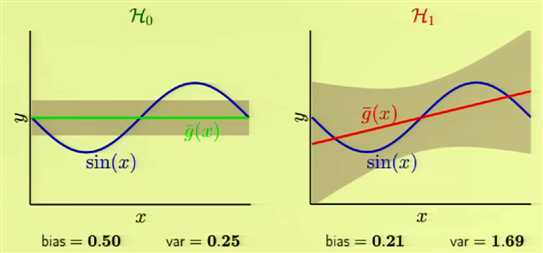
假设使用两个假设集去学习正弦函数,数据集是正弦函数上的随机的两个点(使用平方误差)

\(H_0\): h(x)=b

\(H_1\): h(x)=ax+b

\(\overline{g}(x)\)是指平均假设,灰色区域是方差,平均假设和目标函数间的距离就是偏差

模型的复杂度取决于数据集而不是目标函数的复杂度,数据集决定了你能做到多好,目标函数的复杂度只决定了问题的难度

偏差与方差

原文：https://www.cnblogs.com/redo19990701/p/11393294.html