线性回归

变量描述

线性回归模型

线性回归,回归是指实值输出

线性回归尝试得到输入与输出的线性联系

• \(s=\sum_{i=0}^dw_ix_i\)
  • \(w_i\)是指作用于输入\(x_i\)的权值
  • 规定\(x_0\)等于1,这样\(w_0\)就是偏差\(b\)
• \(h(\mathtt x)=s=\sum_{i=0}^dw_ix_i=\mathtt{w^Tx}\)
  • \[\mathtt x=\begin{bmatrix} {x_0}\{x_1}\{\vdots}\{x_d}\\end{bmatrix}\] \(\mathtt x\in R^{(d+1)*1}\),\[\mathtt w=\begin{bmatrix} {w_0}\{w_1}\{\vdots}\{w_d}\\end{bmatrix}\] \(\mathtt w\in R^{(d+1)*1}\)

误差测量

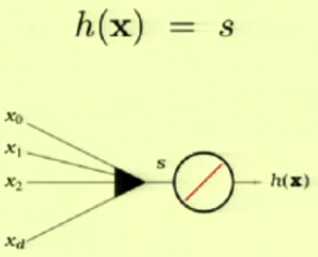
这里使用平方误差\((h(\mathtt x)-f(\mathtt x))^2\)

\(E_{in}(\mathtt w)=\frac{1}{N}\sum_{n=1}^{N}(h(\mathtt x)-y_n)^2\)

? \(=\frac{1}{N}\sum_{n=1}^{N}(\mathtt{w^Tx_n-}y_n)^2\)$

? \(=\frac{1}{N}||\mathtt{Xw-y}||^2\)

\(\mathtt X=\begin{bmatrix} {\mathtt x_1^T}\\ {\mathtt x_2^T}\\ {\vdots}\\ {\mathtt x_N^T}\\\end{bmatrix}\) \(\mathtt X\in R^{N*(d+1)}\),\(\mathtt y=\begin{bmatrix} {y_1}\\ {y_2}\\ {\vdots}\\ {y_N}\\\end{bmatrix}\) \(\mathtt y\in R^{N*1}\)

令其导数为零即可得到解

\(\nabla E_{in}(\mathtt w)=\frac{2}{N}\mathtt X^T(\mathtt{Xw-y})=0\)

\(\mathtt{X^TXw=X^Ty}\)

\(\mathtt{w=(X^TX)^{-1}X^Ty}\)

\(\mathtt{(X^TX)^{-1}X^T}\)称作\(\mathtt X\)得伪逆矩阵,因为\(\mathtt{X}\)往往不是一个方矩阵

线性回归算法伪代码

总结

这也称作一步学习,因为只需求出输入矩阵的为逆矩阵学习就差不多结束了

线性回归就像是一辆公交车,很方便,虽然不会让你觉着威风.

线性回归也可以作为其他方法权值的初始化,例如PLA,虽然这不是最好的结果,但是一个相对较好的结果,如果PLA使用随机的权值开始到达这个较好的结果会花费很多时间,线性回归的性质使得这一步很容易到达.而且从一个较好的权值开始,PLA也会很快的收敛到最优解或者局部最优解

线性回归

原文：https://www.cnblogs.com/redo19990701/p/11398740.html