如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
7
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
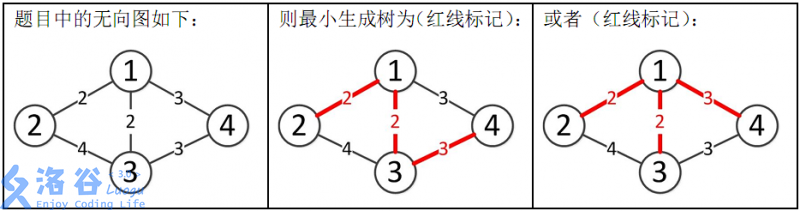
所以最小生成树的总边权为2+2+3=7
真的就是一道最小生成树的裸题啊
敬爱的读者可以先看一看这一篇博客中的讲解哦
#include<bits/stdc++.h> #define maxn 5005 #define maxm 200005 using namespace std; int n,m; struct edge{ int x,y,v; }e[maxm]; int cmp(edge a,edge b) { return a.v<b.v; } int fa[maxn]; int find(int x) { if(x==fa[x]) return x; x=find(fa[x]); return fa[x]; } int Kruskal() { for(int i=1;i<=n;i++) fa[i]=i; sort(e+1,e+m+1,cmp); int cnt=0,ans=0; for(int i=1;i<=m;i++) { int fx=find(e[i].x),fy=find(e[i].y); if(fx==fy) continue; fa[fx]=fy; ++cnt; ans+=e[i].v; if(cnt==n-1) break; } return ans; } int main() { scanf("%d%d",&n,&m); for(int i=1,x,y,z;i<=m;i++) { scanf("%d%d%d",&x,&y,&z); e[i].x=x; e[i].y=y; e[i].v=z; } cout<<Kruskal(); return 0; }
原文:https://www.cnblogs.com/Tidoblogs/p/11406130.html