本节课我们来学习本章的第一个难点,就是B树。那么B树它其实是一种数据结构,我们设计出这种数据结构就是为了提高我们的查找效率的,提高我们在磁盘上的查找效率。那么什么是B树呢?了解B树之前,我们先来回忆一下第四章学习过的一种特殊二叉树,就是平衡二叉树。
平衡二叉树的定义是,任意结点的左右子树高度之差的绝对值均不超过1。这样特殊的二叉树我们称之为平衡二叉树。因为我们有了平衡二叉树这样一种特殊的二叉树,所以我们在平衡二叉树上的查找,不会退化为一种线性结构,也就是不会退化为在线性结构上的查找。所以,它的查找效率会比较的高。那么,我们根据平衡二叉树的特点,做出了一些改进,就设计出了B树。
在平衡二叉树当中,每个结点只有一个关键字一个数据元素。
那么在B树中,每个结点可以有多个数据元素,可以有多个关键字。好,我们简单地了解了一下什么是B树。接下来,我们就来看一下书中严格的定义。
书中是这样定义B树的,又称为多路平衡查找树。B树中所有结点孩子结点数的最大值称为B树的阶。这里也需要给大家强调的是,一定要记作为孩子结点数的最大值。因为有的时候我们会记错,会把它记错为关键字的数量的最大值。所以再次强调,一定是所有结点的孩子结点数的最大值为B树的阶。
好,除了这一个特点之后,我们再来看一下B树还有哪些要求?一棵m阶B树,或为空树,或为满足如下特性的m叉树。那么其实对B树的要求非常多,没关系,我们先来总览一下,然后再逐条地在例子当中看一下它有哪些要求。
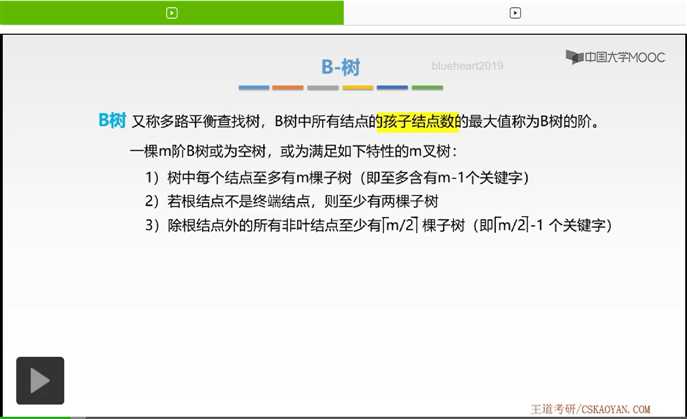
首先第一条是树中每个结点至多有m棵子树,即至多含有m-1个关键字。大家发现了,这里关键字,也就是我们存储的数据元素的数量,是不是子树的数量、分支的数量减1啊,我们有这样的要求。
接下来,若根结点不是终端结点。也就是说,如果该B树当中,不仅仅只有一个终端结点的话,则它至少有两棵子树。根结点至少有两棵子树,也就是至少有一个关键字呗,我们根据性质1知道。
那么第三条则是除根结点外的所有非叶结点至少有[m/2](m/2取上阶)棵子树,这里我们对每一个非叶结点的子树数量是有要求的,它至少有[m/2](m/2取上阶)棵子树。那么接下来我们根据性质1,则它至少有[m/2]-1(m/2取上阶减1个关键字),这是我们根据性质1得到的。好,这就是B树的前三条要求。那么要求到这儿,同学们一定会有疑问。在每个结点上我们都会有多个关键字,也会有指向多棵子树根结点的指针,那么这些指针以及关键字是如何进行放置的呢?
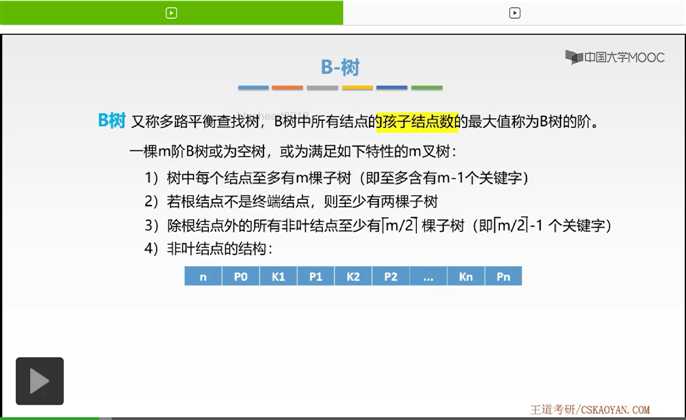
接下来我们就来看一下,非叶结点的结构。这就是B树当中非叶结点的结构。我们来看一下,它其实存放在一个数组当中。这里数组的第一个值存放的是结点关键字的个数n,那么这个n它有范围是不是啊。因为我们对每个结点它是关键字是有要求的,它一定是小于等于m-1。为什么小于等于m-1啊,因为它是m阶的B树。如果它的关键字大于m-1的话,它就不再是一棵m阶的B树了。其次它还要大于等于[m/2]-1(m/2取上阶减1)。因为我们在要求3上对关键字的数量有这样一个最小值的要求。好,这就是第一个值n,它存放的是关键字的个数。接下来我们就来放置指向子树根节点的指针以及关键字了,我们是这样放置的。首先我们放置了一个P0,它是指向第一个子树根结点的指针,然后我们放置第二个值是一个关键字K1。其次我们又放置了一个指向子树根结点的指针P1,然后我们放置了关键字P2。这样的交错依次放置,最后一个放置的是指向一个子树根结点的指针Pn。除了有这样放置的要求以外,还有哪些要求呢?
那么还有这样要求。对于关键字来讲,
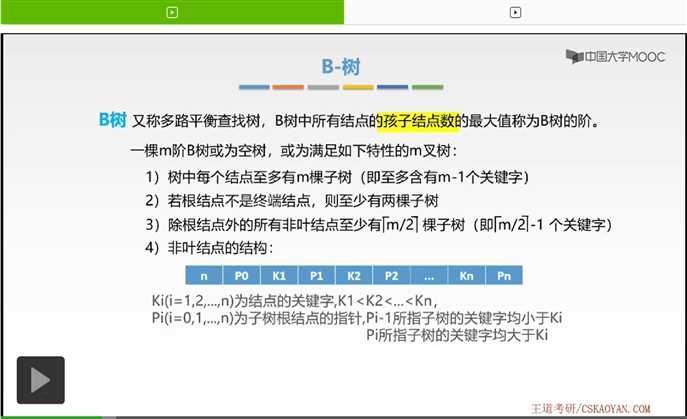
原文:https://www.cnblogs.com/ZHONGZHENHUA/p/11409657.html