Prim和Kruskal都是针对无向图而言的
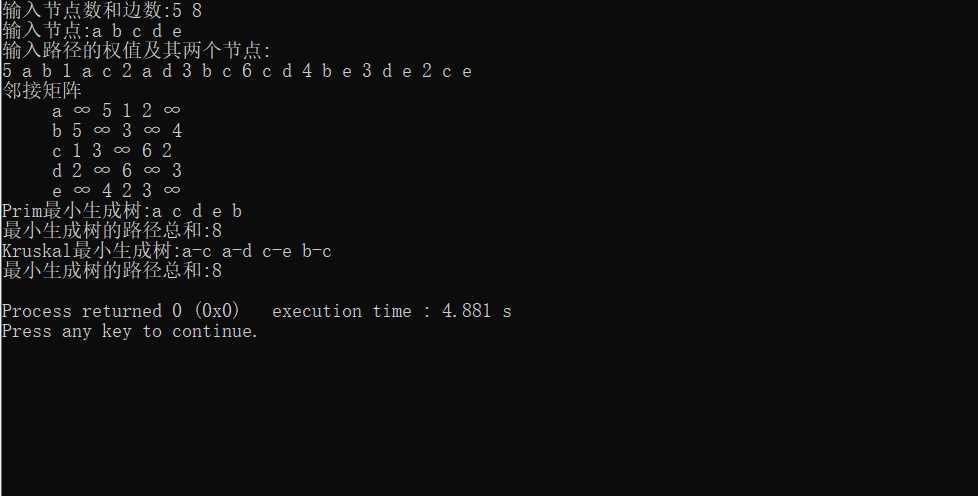
以5 a b 1 a c 2 a d 3 b c 6 c d 4 b e 3 d e 2 c e生成有权无向图,并生成最小生成树
#include <stdio.h> #include <stdlib.h> #define MaxVertexNum 100 #define BIG 100 typedef char VertexType;//顶点节点的数据类型 typedef int EdgeType;//边权值的数据类型 typedef struct{ VertexType Vertex[MaxVertexNum];//顶点表 EdgeType Edge[MaxVertexNum][MaxVertexNum];//邻接矩阵,边表 int vertexnum,arcnum;//顶点数和边数 }MGraph;//邻接矩阵的存储结构 int Locate(VertexType v){ if(v>=97){return (int)v-97;} else {return (int)v-65;} }//将顶点转换为相应的位置 typedef struct{ int a,b;//a和b一条边所连的两个顶点 EdgeType w;//边的权值 }Road,RoadList[MaxVertexNum]; void CreatGraph(MGraph &M,Road RoadList[]){ EdgeType e; VertexType v1,v2; printf("输入节点数和边数:"); scanf("%d %d",&M.vertexnum,&M.arcnum); printf("输入节点:"); for(int i=0;i<M.vertexnum;i++){ getchar(); scanf("%c",&M.Vertex[i]); } for(int i=0;i<M.vertexnum;i++){ for(int j=0;j<M.vertexnum;j++){ M.Edge[i][j]=BIG; } } fflush(stdin);//清除缓存,防止下一次的scanf()函数失效 printf("输入路径的权值及其两个节点:\n"); for(int i=0;i<M.arcnum;i++){ scanf("%d %c %c",&e,&v1,&v2); M.Edge[Locate(v1)][Locate(v2)]=e; M.Edge[Locate(v2)][Locate(v1)]=e; RoadList[i].w=e; RoadList[i].a=Locate(v1); RoadList[i].b=Locate(v2); } }//构造一个有向图 void PrintGraph(MGraph &M){ printf("邻接矩阵\n"); for(int i=0;i<M.vertexnum;i++){ printf(" %c ",M.Vertex[i]); for(int j=0;j<M.vertexnum;j++){ if(M.Edge[i][j]!=BIG){ printf("%d ",M.Edge[i][j]); } else{printf("∞ ");} } printf("\n"); } }//打印邻接矩阵 void visited(int v){ printf("%c ",v+‘a‘); }//访问当前节点的位置 void Prim(MGraph &M,VertexType c){ int v0=Locate(c); int vertexvisit[M.vertexnum];//记录已经访问的顶点 int lowcost[MaxVertexNum];//当前生成树到剩余顶点的最短边的权值 int v,min,sum=0,k;//sum表示当前累计树的权值 for(int i=0;i<M.vertexnum;i++){ vertexvisit[i]=0; lowcost[i]=M.Edge[v0][i]; if(lowcost[i]==0){lowcost[i]=10;} } vertexvisit[v0]=1; printf("Prim最小生成树:"); visited(v0); for(int i=0;i<M.vertexnum-1;i++){ min=10;//找最小的边,初值设为大于全部边的权值 for(int j=0;j<M.vertexnum;j++){ if(vertexvisit[j]==0&&lowcost[j]<min){ min=lowcost[j]; k=j;//记录当前的位置 } } vertexvisit[k]=1; v=k; visited(v); sum=sum+min; for(int j=0;j<M.vertexnum;j++){ if(vertexvisit[j]==0&&M.Edge[v][j]<lowcost[j]){ lowcost[j]=M.Edge[v][j];//将刚并入的顶点为媒介更新候选边 } } } printf("\n最小生成树的路径总和:%d\n",sum); }//Prim算法构造最小生成树 int ver[MaxVertexNum];//定义并查集 int getRoot(int a){ while(a!=ver[a])a=ver[a]; return a; }//在并查集中查找根节点 void sort(Road RoadList[],int m){ Road temp; for(int i=0;i<m;i++){ for(int j=0;j<m-1-i;j++){ if(RoadList[j].w>RoadList[j+1].w){ temp=RoadList[j]; RoadList[j]=RoadList[j+1]; RoadList[j+1]=temp; } } } }//将图中所有边按其权值从大到小排序 void Kruskal(MGraph &M,Road RoadList[]){ int sum=0; int a,b; for(int i=0;i<M.vertexnum;i++){ ver[i]=i; } sort(RoadList,M.arcnum); printf("Kruskal最小生成树:"); for(int i=0;i<M.arcnum;i++){ a=getRoot(RoadList[i].a); b=getRoot(RoadList[i].b); if(a!=b){ ver[a]=b; sum=sum+RoadList[i].w; printf("%c-%c ",RoadList[i].a+‘a‘,RoadList[i].b+‘a‘); } } printf("\n最小生成树的路径总和:%d\n",sum); }//Kruskal构造最小生成树 int main(){ MGraph M; Road RoadList[MaxVertexNum]; CreatGraph(M,RoadList); PrintGraph(M); Prim(M,‘a‘); Kruskal(M,RoadList); }
原文:https://www.cnblogs.com/Yshun/p/11409221.html