罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个罗马数字,将其转换成整数。输入确保在 1 到 3999 的范围内
示例 1:
输入: "III"
输出: 3
示例 2:
输入: "IV"
输出: 4
示例 3:
输入: "IX"
输出: 9
示例 4:
输入: "LVIII"
输出: 58
解释: L = 50, V= 5, III = 3.
示例 5:
输入: "MCMXCIV"
输出: 1994
解释: M = 1000, CM = 900, XC = 90, IV = 4.
解题思路: 1.构建一个字典记录所有罗马数字子串,注意长度为2的子串记录的值是(实际值 - 子串内左边罗马数字代表的数值) int RomanToInt(string s) { unordered_map<string, int> stMap = {{"I", 1}, {"IV", 3}, {"IX", 8}, {"V", 5}, {"X", 10}, {"XL", 30}, {"XC", 80}, {"L", 50}, {"C", 100}, {"CD", 300}, {"CM", 800}, {"D", 500}, {"M", 1000}}; int iSum = stMap[s.substr(0, 1)]; for (int i = 1; i < (int)s.size(); i++) { string szOne = s.substr(i, 1); string szTwo = s.substr(i - 1, 2); iSum += stMap[szTwo] ? stMap[szTwo] : stMap[szOne]; } return iSum; }
Data is the currency of today‘s web, mobile, social, enterprise and cloud applications. Ensuring data is always available is a top priority for any organization - minutes of downtime will result in significant loss of revenue and reputation.
数据是当今网络、手机、社交、企业和云应用的货币;确保数据始终可用是任何组织首要的任务 -- 停机几分钟将导致收入和声誉严重的损失。
This Guide is designed to assist Developers, Architects and DBAs understanding, implementing and managing MySQL InnoDB Cluster, an integrated, native, HA solution for your MySQL databases.
原文链接:https://zhuanlan.zhihu.com/p/36274119
既然问的是STL的sort算法实现,那么先确认一个问题,哪些STL容器需要用到sort算法?
首先,关系型容器拥有自动排序功能(相对key值),因为底层采用RB-Tree,所以不需要用到sort算法。
其次,序列式容器中的stack、queue和priority-queue都有特定的出入口,不允许用户对元素排序。
剩下的vector、deque,适用sort算法。
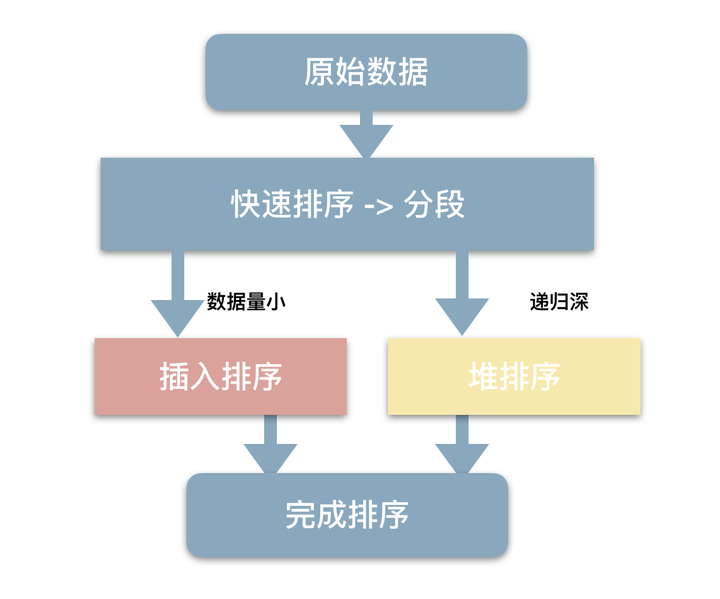
STL的sort算法,数据量大时采用QuickSort快排算法,分段归并排序。一旦分段后的数据量小于某个门槛(16),为避免QuickSort快排的递归调用带来过大的额外负荷,就改用Insertion Sort插入排序。如果递归层次过深,还会改用HeapSort堆排序。
具体代码 源文件:/usr/include/c++/4.2.1/bits/stl_algo.h template <class _RandomAccessIter, class _Compare> template <class _RandomAccessIter, class _Compare> inline void sort(_RandomAccessIter __first, _RandomAccessIter __last, _Compare __comp) { __STL_REQUIRES(_RandomAccessIter, _Mutable_RandomAccessIterator); __STL_BINARY_FUNCTION_CHECK(_Compare, bool, typename iterator_traits<_RandomAccessIter>::value_type, typename iterator_traits<_RandomAccessIter>::value_type); if (__first != __last) { // 快速排序 + 堆排序 __introsort_loop(__first, __last, __VALUE_TYPE(__first), __lg(__last - __first) * 2, __comp); // 插入排序(当排序个数 <= 16) __final_insertion_sort(__first, __last, __comp); } } template <class _RandomAccessIter, class _Tp, class _Size, class _Compare> void __introsort_loop(_RandomAccessIter __first, _RandomAccessIter __last, _Tp *, _Size __depth_limit, _Compare __comp) { // 当排序的数量大于16 while (__last - __first > __stl_threshold) { // 递归深度为0时,调用堆排序 if (__depth_limit == 0) { partial_sort(__first, __last, __last, __comp); return; } --__depth_limit; // 快速排序 // 1.找基准元素 _RandomAccessIter __cut = __unguarded_partition(__first, __last, _Tp(__median(*__first, *(__first + (__last - __first) / 2), *(__last - 1), __comp)), __comp); // 分治思想:递归排序 __introsort_loop(__cut, __last, (_Tp *)0, __depth_limit, __comp); __last = __cut; } } // 堆排序 template <class _RandomAccessIter, class _Tp, class _Compare> void __partial_sort(_RandomAccessIter __first, _RandomAccessIter __middle, _RandomAccessIter __last, _Tp *, _Compare __comp) { make_heap(__first, __middle, __comp); for (_RandomAccessIter __i = __middle; __i < __last; ++__i) if (__comp(*__i, *__first)) __pop_heap(__first, __middle, __i, _Tp(*__i), __comp, __DISTANCE_TYPE(__first)); sort_heap(__first, __middle, __comp); } // 插入排序 template <class _RandomAccessIter, class _Compare> void __final_insertion_sort(_RandomAccessIter __first, _RandomAccessIter __last, _Compare __comp) { if (__last - __first > __stl_threshold) { __insertion_sort(__first, __first + __stl_threshold, __comp); __unguarded_insertion_sort(__first + __stl_threshold, __last, __comp); } else __insertion_sort(__first, __last, __comp); } // 计算递归深度 template <class _Size> inline _Size __lg(_Size __n) { _Size __k; for (__k = 0; __n != 1; __n >>= 1) ++__k; return __k; }
原文链接:https://zentia.github.io/2018/09/21/TSF4G/
TBUS原理与实现,让程序忽略网路通信;
TBUS实现原理:
Tbus基于共享内存构建无锁双通循环消息队列,发送的双方通过专用的读写队列完成数据收发,实现本地进程或者远程进程间通信。通信双方使用的两个队列称之为tbus通道(channel),每一组通讯的双方就需要有一个tbus通道。
在同一台物理机通讯:
不同物理机之间的通信:
原文:https://www.cnblogs.com/yzdai/p/11409359.html