首页 > 其他 > 详细

Educational Codeforces Round 71 (Rated for Div. 2)

时间：2019-08-27 15:15:26      阅读：52      评论：0      收藏：0      [点我收藏+]

Solution

A. There Are Two Types Of Burgers

题意：
做一个\(A\)需要两个\(b\)和两个\(p\)，能卖\(h\)元；做一个\(B\)需要两个\(b\)和两个\(f\)，能卖\(c\)元。给出\(b,p,f\)的数量，求最多卖多少元。
思路：
比赛的时候用循环搞了，判断\(h,c\)的大小关系，决定先做什么。也可以\(b=b/2\)，然后判断大小，每次取最小值，利润直接算，然后更新\(b\)，再进行一次。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
#define lson (rt<<1)
#define rson (rt<<1|1)
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
int main() {
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    int _,b,p,f;
    double h,c;
    ll ans;
    for(scanf("%d",&_);_;_--) {
        scanf("%d%d%d%lf%lf",&b,&p,&f,&h,&c);
        ans=0;
        if(h>c) {
            while(b>=2&&p) {
                ans+=h;
                b-=2;
                p--;
            }
            while(b>=2&&f) {
                ans+=c;
                b-=2;
                f--;
            }
        } if(h<c) {
            while(b>=2&&f) {
                ans+=c;
                b-=2;
                f--;
            }
            while(b>=2&&p) {
                ans+=h;
                b-=2;
                p--;
            }
        } else {
            int zhi=p+f;
            while(b>=2&&zhi) {
                ans+=h;
                b-=2;
                zhi--;
            }
        }
        printf("%lld\n",ans);
    }
}
//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
int _;
int b,p,f;
int h,c;
 
int main() {
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    for (scanf("%d",&_);_;_--) {
        scanf("%d%d%d%d%d",&b,&p,&f,&h,&c);
        ll ans=0;
        b/=2;
        if (h>c) {
            int x=min(b,p);
            ans+=x*h;
            b-=x,p-=x;
            int y=min(b,f);
            ans+=y*c;
        } else {
            int x=min(b,f);
            ans+=x*c;
            b-=x,f-=x;
            int y=min(b,p);
            ans+=y*h;
        }
        printf("%lld\n",ans);
    }
}

B. Square Filling

题意：
给出一个\(01\)矩阵\(A\)，让你用一个全\(0\)矩阵\(B\)，通过每次选\(2\times2\)的子矩阵设值为\(1\)，把\(B\)变为\(A\)，可以的话，输出你选的子矩阵的左上角坐标。
思路：
范围不大，直接枚举\(1\)的位置，判断周围是否存在全\(1\)子矩阵。
题解思路是存在子矩阵乘积大于0的，就全部设置为\(2\)，然后一直进行，如果最后还有\(1\)，说明不行。

#include <bits/stdc++.h>
#define lowbit(x) (x)&(-x)
#define srand() srand(time(0))
#define pi acos(-1.0)
#define printftime() printf("Time used = %.2f\n",(double)clock()/CLOCKS_PER_SEC)
using namespace std;
typedef long long ll;
int a[100][100];
int flag[100][100];
struct len {
    int l,r;
}ans[100000];
int main()
{
    int n,m,cnt=1;int f=0;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)scanf("%d",&a[i][j]);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j]){
                if(a[i-1][j-1]&&a[i-1][j]&&a[i][j-1]){
                    ans[cnt].l=i-1;
                    ans[cnt++].r=j-1;
                    continue ;
                }
                if(a[i][j-1]&&a[i+1][j]&&a[i+1][j-1]){
                    ans[cnt].l=i;
                    ans[cnt++].r=j-1;
                    continue ;
                }
                if(a[i+1][j+1]&&a[i+1][j]&&a[i][j+1]){
                    ans[cnt].l=i;
                    ans[cnt++].r=j;
                    continue ;
                }
                if(a[i-1][j]&&a[i-1][j+1]&&a[i][j+1]){
                    ans[cnt].l=i-1;
                    ans[cnt++].r=j;
                    continue ;
                }
                f=1;
            }
        }
    }
    if(f)puts("-1");
    else {
        printf("%d\n",cnt-1);
        for(int i=1;i<cnt;i++)printf("%d %d\n",ans[i].l,ans[i].r);
    }
}
//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
int n, m;
int a[100][100];
 
int main() {
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) 
            scanf("%d", &a[i][j]);
    }   
    vector<pair<int, int> > ans;
    for (int i = 1; i < n; i++) {
        for (int j = 1; j < m; j++) {
            if (a[i][j] * a[i][j + 1] * a[i + 1][j] * a[i + 1][j + 1] > 0 ) {
                a[i][j] = a[i][j + 1] = a[i + 1][j] = a[i + 1][j + 1] = 2;
                ans.push_back({i, j});
            }
        }
    }
    bool ok=true;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i][j] == 1) {
                ok = false; break;
            }
        }
    }
    if (!ok) puts("-1");
    else {
        printf("%d\n", (int)ans.size());
        for (int i = 0; i < (int)ans.size(); i++) {
            printf("%d %d\n", ans[i].first, ans[i].second);
        }
    }
    return 0;
}

C. Gas Pipeline

题意：
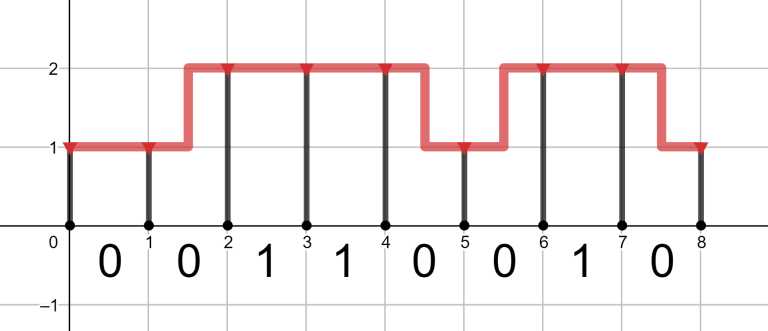
给一条公路用\(01\)字符串表示，有十字路口用\(1\)表示，现在要架管道，十字路口的时候，管道必须在高度为\(2\)的位置，其他位置高度可以为\(1\)，管道同时需要支架，现给出\(01\)字符串，让你给公路架管道，保证开始和结束都是高度为\(1\)的管道。给出单位长度管道的花费和单位高度支架的花费，求架完公路的最小花费。
技术分享图片

思路：
很容易想到贪心，处理出连续\(0\)序列的长度，\(0\)的位置可能不下降，所以判断一下下降与不下降的花费，选择较小的。
\(dalao\)好像都是动态规划写的。\(dp[i][0/1]\)表示\(i\)位置右边支架为\(0/1\)的最小花费，转移的话就，
\[ dp[i][0/1]= \begin{cases} dp[i][0]=min(dp[i-1][0]+a,\ dp[i-1][1]+2{\ast}a)+b, &\text{if s[i]=='0'}\ dp[i][1]=min(dp[i-1][0]+2{\ast}a,\ dp[i-1][1]+a)+2{\ast}b, &\text{if s[i]=='0'}\ dp[i][1]=dp[i-1][1]+a+2{\ast}b, &\text{if s[i]=='1'}\ dp[i][0]=INF,& \text{if s[i]=='1'} \end{cases} \]
当\(s[i]=1\)的时候，右边支架高度只能为2，所以\(dp[i][0]=INF\)，并且只能由\(d[i-1][1]\)转移得到，因为左边支架高度也只能为\(2\)。初始\(dp[0][0]=b,dp[0][1]=INF\)，因为左边由高度为\(1\)开始的。答案即为\(dp[n][0]\)。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
#define lson (rt<<1)
#define rson (rt<<1|1)
const int N=100010;
const int inf=0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
char s[2*N];
ll d[2*N];
 
int main() {
    #ifdef DEBUG
    freopen("in.txt","r",stdin);
    #endif
    int _,len;
    ll a,b;
    for(scanf("%d",&_);_;_--) {
        scanf("%d%lld%lld",&len,&a,&b);
        scanf("%s",s+1);
        d[len+1]=0;
        for(int i=len;i>=1;i--) {
            if(s[i]=='1') d[i]=0;
            else d[i]=d[i+1]+1;
        }
        //for(int i=1;i<=len;i++) printf("%d",d[i]);
        int op=0; //下降态
        ll sum=0;
        ll cnt=0; // 支柱：0但不下降
        for(int i=1;i<=len;i++) {
            if(s[i]=='0') {
                if(op) {
                    if(2*a-d[i]*b+b<=0||i+d[i]-1==len) { //下降
                        if(i+d[i]-1==len) { //最后下
                            sum+=(d[i]+2)*a;
                            cnt+=2*b;
                            cnt+=d[i]*b;
                        } else { //中间下
                            sum+=(d[i]+1)*a;
                            cnt+=(d[i]-1)*b;
                            cnt+=2*b;
                        }
                        op=!op;
                    } else { // 不下降
                        sum+=d[i]*a;
                        cnt+=d[i]*2*b;
                    }
                } else {
                    if(i+d[i]-1!=len) {
                        sum+=(d[i]-1)*a;
                        cnt+=d[i]*b;
                    } else {
                        sum+=d[i]*a;
                        cnt+=(d[i]+1)*b;
                    }
                }
                i=i+d[i]-1;
            } else {
                if(op) {
                    sum+=a;
                } else {
                    sum+=2*a;
                    op=!op;
                }
                cnt+=2*b;
            }
            //printf("i=%d   %lld  **** %lld\n",i,sum,cnt);
        }
        sum=sum+cnt;
        printf("%lld\n",sum);
    }
}
//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
const int inf = 0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
char s[2*N];
ll dp[2*N][2];
int _;
int n;
ll a, b;
 
int main() {
    #ifdef DEBUG    
    freopen("in.txt", "r", stdin);
    #endif
    for (scanf("%d", &_); _; _--) {
        scanf("%d %lld %lld", &n, &a, &b);
        scanf("%s", s+1);
        dp[0][0] = b; dp[0][1] = INF;
        for (int i = 1; i <= n; i++) {
            if (s[i] == '0') {
                dp[i][1] = min(dp[i - 1][1] + a + 2 * b, dp[i - 1][0] + 2 * a + 2 * b);
                dp[i][0] = min(dp[i - 1][1] + 2 * a + b, dp[i - 1][0] + a + b);
            } else {
                dp[i][0] = INF;
                dp[i][1] = dp[i - 1][1] + a + 2 * b;
            }
        }
        printf("%lld\n", dp[n][0]);
    }
    return 0;    
}

D. Number Of Permutations

题意：
给出\(n\)个有序对\((x_i,y_i)\)，如果一组有序对，按\(x_i\)排序非递减或按\(y_i\)排序非递减的话定义为坏的。然后问\(n\)的全排列生成的每组有序对有多少个好的。比如\(n=3\)，给出\((1,2),(3,2),(3,1)\)，那么按全排列生成的即为：
\(123 ：(1,2),(3,2),(3,1)\)；
\(132：(1,3),(3,1),(3,2)\)；
\(\vdots\)
思路：
逆向思维，一共有\(n!\)种结果，定义\(cnt_1\)为按\(x_i\)排序非递减的，定义\(cnt_2\)为按\(y_i\)排序非递减的，定义\(cnt_{12}\)为\(x_i和y_i\)同时非递减的。那么答案就是\(n!-cnt_1-cnt_2+cnt_{12}\)。
\(cnt_1\)的求法：假设这么一个序列：\(1,2,1,3\)，全排列后只有两个非递减的，即\(2!\)。再比如：\(1,2,3,2,1\)，全排列后有\(2!\ {\ast}\ 2!\)个非递减的。因为\(1、2\)重复。所以\(cnt_1\)就出来了。\(cnt_2\)同理。
\(cnt_{12}\)的求法：我们可以先按\(x_i\)排序再按\(y_i\)排序，同样也是统计重复的个数。但最后要检查是否满足\(y_i\)非递减。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
const int inf = 0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 998244353;
typedef long long ll;
 
pair<int, int> d[3 * N];
map<int, int> a, b;
map<pair<int, int>, int> ab;
int n;
int fac[3 * N];
 
 
int main() {
    #ifdef DEBUG
    freopen("in.txt", "r", stdin);
    #endif
    scanf("%d", &n);
    fac[0] = 1;
    for (int i = 1; i <= n; i++) {
        fac[i] = 1ll * fac[i - 1] * i % mod;
        scanf("%d %d", &d[i].first, &d[i].second);
        a[d[i].first]++; b[d[i].second]++;
        ab[d[i]]++;       
    }
    sort(d + 1, d + n + 1);
    int sum = fac[n];
    int temp = 1;
    for (auto i : a) {
        temp = 1ll * temp * fac[i.second] % mod;
    }
    sum = (sum - temp + mod) % mod; 
    temp = 1;
    for (auto i : b) {
        temp = 1ll * temp * fac[i.second] % mod;
    }
    sum = (sum - temp + mod) % mod; 
    bool ok = true;
    temp = 1;
    for (auto i : ab) {
        temp = 1ll * temp * fac[i.second] % mod;
    }
    for (int i = 1; i < n; i++) {
        if(d[i].second > d[i + 1].second) {
            ok = false; break;
        }
    }
    if(ok) sum = (sum + temp) % mod;
    printf("%d\n", sum);
}

E. XOR Guessing

题意：
猜数字\(w\)，你每次询问\(100\)个数，会给你一个\(w\)与其中一个的异或结果\(x\)，再次询问\(100\)个数，又给你一个\(w\)与其中一个的异或结果\(y\)，最多询问两次，且你询问的所有数字不能重复，求\(w\)。
思路：
很神奇的思路，\(w\)范围最多\(14\)位二进制，我们可以先用\(100\)个低\(7\)的数字询问，那么\(x\)的高\(7\)位就是\(w\)的高\(7\)位，再用高\(7\)位的数字询问，那么\(y\)的低\(7\)位就是\(w\)的低\(7\)位。\(1\sim100\)刚好能用低\(7\)位表示，然后可以把\(1{\sim}100\)的数字左移\(7\)位，就生成高\(7\)位的数字了。

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
const int inf = 0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
int main() {
    #ifdef DEBUG
    freopen("in.txt", "r", stdin);
    #endif
    printf("?");
    for (int i = 0; i < 100; i++) printf(" %d", i + 1);
    puts("");
    fflush(stdout);
    int x;
    scanf("%d", &x);
    printf("?");
    for (int i = 0; i < 100; i++) printf(" %d", i + 1 << 7);
    puts("");
    fflush(stdout);
    int y;
    scanf("%d", &y);
    printf("! %d", (x & ~0x7f) | (y & 0x7f));
}

F. Remainder Problem

题意：
给出\(a_1,a_2,{\dots},a_{500000}\)，且全为\(0\)，然后有\(q\)次询问，

  • 1 \(x \ y\) :\(a_x + y\)
  • 2 \(x\ y\)：\(\sum_{i{\in}R(x,y)}a_i\)，\(R(x,y)\)是\(1{\sim}500000\)的下标\(i\%x=y\)的集合

思路：
看题解是根号分治，题目大多是\(q\)和\(N\)同一数量级 ，每次修改在原数组上修改，同时用数组预处理出小于\(\sqrt(N)\)的查询\(O(sqrt(N))\)，大于\(\sqrt(N)\)的查询就累加原数组的值\(O({\frac{N}{X}})\)，其中\(X>{\sqrt(N)}\)，所以总复杂度\(O(N{\sqrt(N)})\)。
见代码

//#define DEBUG
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
const int inf = 0X3f3f3f3f;
const long long INF = 0x3f3f3f3f3f3f3f3f;
const double eps = 1e-6;
const double pi = acos(-1.0);
const int mod = 1000000007;
typedef long long ll;
 
int q;
int a[5*N];
int d[710][710];
 
int main() {
    #ifdef DEBUG
    freopen("in.txt", "r", stdin);
    #endif
    scanf("%d", &q);
    int op, x, y;
    for (int i = 1; i <= q; i++) {
        scanf("%d %d %d", &op, &x, &y);
        if (op == 1) {
            a[x] += y;
            for (int j = 1; j < 710; j++) {
                d[j][x % j] += y; //d[j][模j的余数]
            }
        } else {
            int ans = 0;
            if (x < 710) ans = d[x][y]; // d[x][模x的余数=y]
            else {
                for (int j = y; j <= 500000; j += x) {
                    ans += a[j];
                }
            }
            printf("%d\n", ans);
        }
    }
}

Educational Codeforces Round 71 (Rated for Div. 2)

原文：https://www.cnblogs.com/ACMerszl/p/11418228.html
踩
(0)
赞
(0)
   
举报
评论 一句话评论（0）
分享档案
更多>
2021年09月23日 (328)
2021年09月24日 (313)
2021年09月17日 (191)
2021年09月15日 (369)
2021年09月16日 (411)
2021年09月13日 (439)
2021年09月11日 (398)
2021年09月12日 (393)
2021年09月10日 (160)
2021年09月08日 (222)
最新文章
更多>
教程昨日排行
更多>
友情链接
汇智网   PHP教程   插件网  
关于我们 - 联系我们 - 留言反馈 - 联系我们:wmxa8@hotmail.com
© 2014 bubuko.com 版权所有
打开技术之扣，分享程序人生！