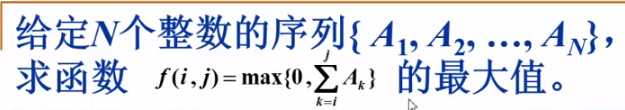
// 求最大子列和
#include <cstdio>
int a[5];
// O(n^3)
int MaxSeq1(int a[], int n)
{
int max = 0, sum = 0;
for(int i = 0; i < n; ++ i)
{
for(int j = i; j < n; ++ j)
{
sum = 0;
for(int k = i; k <= j; ++ k)
{
sum += a[k];
}
if(sum > max) max = sum;
}
}
return max;
}
// O(n^2)
int MaxSeq2(int a[], int n)
{
int max = 0, sum = 0;
for(int i = 0; i < n; ++ i)
{
sum = 0;
for(int j = i; j < n; ++ j)
{
sum += a[j];
if(sum > max) max = sum;
}
}
return max;
}
// 在线处理 O(n)
// "在线"的意思是指每输入一个数据就进行及时处理
// 在任何一个地方终止输入, 算法都能正确给出当前解
int MaxSeq4(int a[], int n)
{
int sum = 0, max = 0;
for(int i = 0; i < n; ++ i)
{
sum += a[i];
if(sum > max) max = sum;
else if(sum < 0) sum = 0;
}
return max;
}
int main()
{
for(int i = 0; i < 5; ++ i)
{
scanf("%d", &a[i]);
}
printf("%d\n", MaxSeq4(a, 5));
return 0;
}
/*
1 6 -5 9 -3
11
*/
原文:https://www.cnblogs.com/mjn1/p/11420267.html