Description
Input
Output
Sample Input
7 2 1 4 5 1 3 3 4 1000 1000 1000 1000 0
Sample output
8
4000
翻译
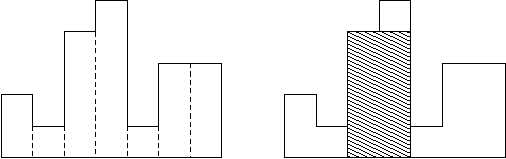
柱状图是一个多边形,由一系列在公共基线上对齐的矩形组成。矩形的宽度相等,但高度不同。例如,左侧的图显示了由高度为2、1、4、5、1、3、3的矩形组成的直方图,以单位度量,其中1是矩形的宽度:
通常,柱状图用于表示离散分布,例如文本中字符的频率。请注意,矩形的顺序,即它们的高度,非常重要。计算柱状图中最大矩形的面积,该柱状图也与公共基线对齐。右图显示了所示直方图的最大对齐矩形。
输入
输入包含几个测试用例。每个测试用例描述一个柱状图,以一个整数n开头,表示它所组成的矩形的数量。您可以假设1<=n<=100000。然后跟随n个整数h1,…,hn,其中0<=hi<=100000000。这些数字表示从左到右的柱状图矩形的高度。每个矩形的宽度为1。最后一个测试用例的输入后面跟着一个零。
输出
对于单行上的每个测试用例输出,指定柱状图中最大矩形的面积。记住,这个矩形必须与公共基线对齐。
这道题网上大多是用单调栈,然而我觉得这道题用单调队列和单调栈都是一样的
这个矩形肯定是以某一个为基准向两边扩展的
我们可以对某一个柱子的高度为标准,尽量的向两头扩展,这样就可以找出以它高度为标准的,并包含它本身的最大矩形。然后对每一个柱子都做类似的工作,最后挑出里面最大的矩形。
有没有跟动规里面最大子矩阵的一个方法很像?
最后注意细节

1 /************************ 2 User:Mandy.H.Y 3 Language:c++ 4 Problem:POj 2559 5 Algorithm: 6 ************************/ 7 //#include<bits/stdc++.h> 8 #include<cstdio> 9 #include<iomanip> 10 #include<cmath> 11 12 using namespace std; 13 14 const int maxn = 1e5 + 5; 15 16 int n,l,r; 17 int q[maxn]; 18 19 struct Node{ 20 int h,l,r; 21 }node[maxn]; 22 23 template<class T>inline void read(T &x){ 24 x = 0;bool flag = 0;char ch = getchar(); 25 while(!isdigit(ch)) flag |= ch == ‘-‘,ch = getchar(); 26 while(isdigit(ch)) x = (x << 1) + (x << 3) + (ch ^ 48),ch = getchar(); 27 if(flag) x = -x; 28 } 29 30 template<class T>void putch(const T x){ 31 if(x > 9) putch(x / 10); 32 putchar(x % 10 | 48); 33 } 34 35 template<class T>void put(const T x){ 36 if(x < 0) putchar(‘-‘),putch(-x); 37 else putch(x); 38 } 39 40 void file(){ 41 freopen("2559.in","r",stdin); 42 // freopen("1090.out","r",stdin); 43 } 44 45 void work(){ 46 read(n); 47 while(n){ 48 long long ans = 0; 49 for(int i = 1;i <= n; ++ i) read(node[i].h),node[i].l = i,node[i].r = i; 50 //初始化l,r 51 l = r = 0; 52 for(int i = 1;i <= n; ++ i){ 53 while(l < r && node[q[r - 1]].h >= node[i].h) node[i].l = node[q[r - 1]].l,r--; 54 //q中存的是编号,更新时 node[i].l = node[q[r - 1]].l,也可以是剩下的那个坐标 +1,但是要判空 55 q[r++] = i; 56 } 57 l = r = 0; 58 for(int i = n; i >= 1; -- i){ 59 while(l < r && node[q[r - 1]].h >= node[i].h) node[i].r = node[q[r - 1]].r,r--; 60 q[r++] = i; 61 ans = max(ans,(long long)node[i].h * (node[i].r - node[i].l + 1)); 62 } 63 put(ans); 64 putchar(‘\n‘); 65 read(n); 66 } 67 } 68 69 int main(){ 70 // file(); 71 work(); 72 return 0; 73 }
POJ 2559 Largest Rectangle in a Histogram
原文:https://www.cnblogs.com/Mandy-H-Y/p/11420282.html