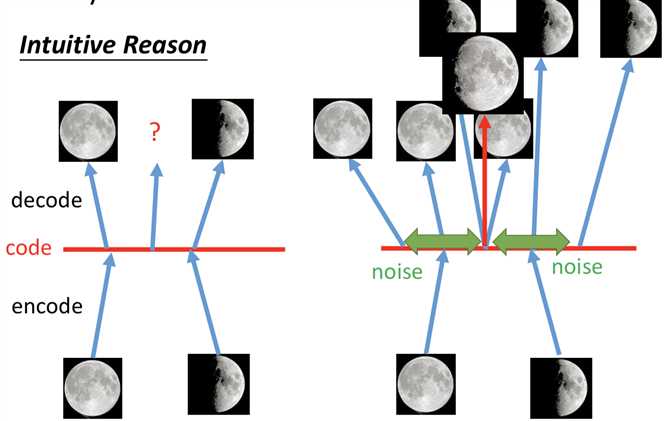
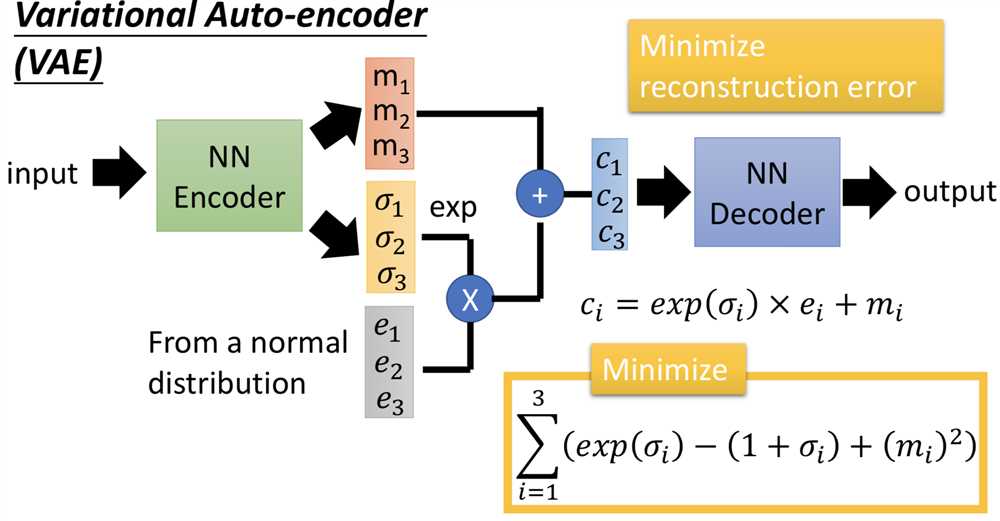
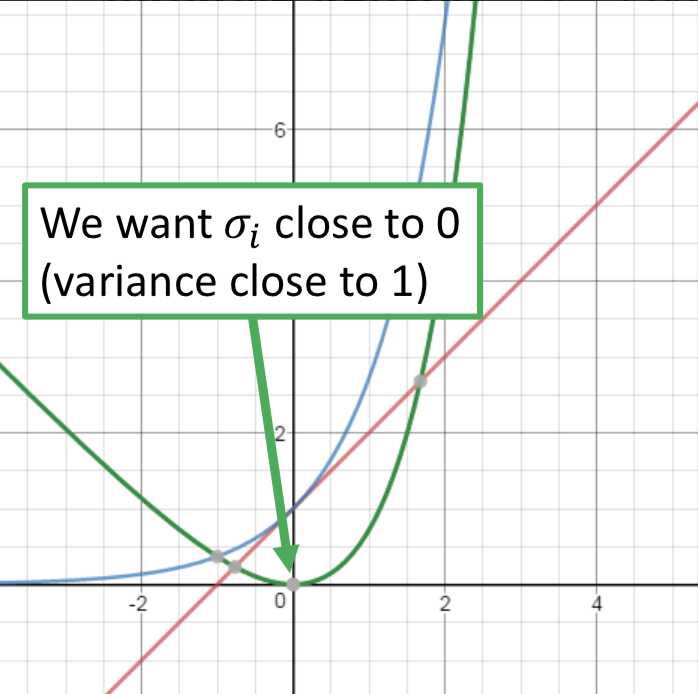
因此在VAE中,encoder输出的不直接是code,而是一组m和一组σ,而向量c才是真正的加了噪声的code,其中ci = exp(σi) x ei + mi。训练过程中的优化目标也不仅是重构误差,还有一项 Σ (exp(σi) - (1+σi) + (mi)2),要强迫加噪声的方差不能太小(因为是模型学习的参数,如果不做限制,为了能重构的更好会越更新σi 越使得噪声方差接近0;而实际上我们希望σi 接近0(真正的方差接近1),所以最小化exp(σi) - (1+σi),mi平方项可以理解为L2 norm正则)。
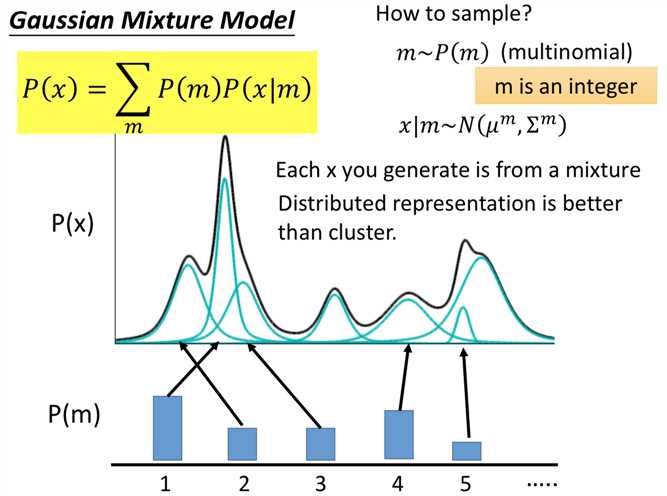
而VAE实际上就是GMM的 distributed representation 的版本,先从一个高斯分布中采样出一个向量z,再根据z来决定mean和variance。那由于 z 是连续的,所以有无穷多个z,就有无穷多个高斯的mean和variance(在GMM中有几个高斯就是固定的)。在z的空间中,每个点都可能被sample到,而每一个点都对应到一个高斯分布。那么如何得到 z 和高斯的mean、variance的对应关系呢?干脆就用一个NN。
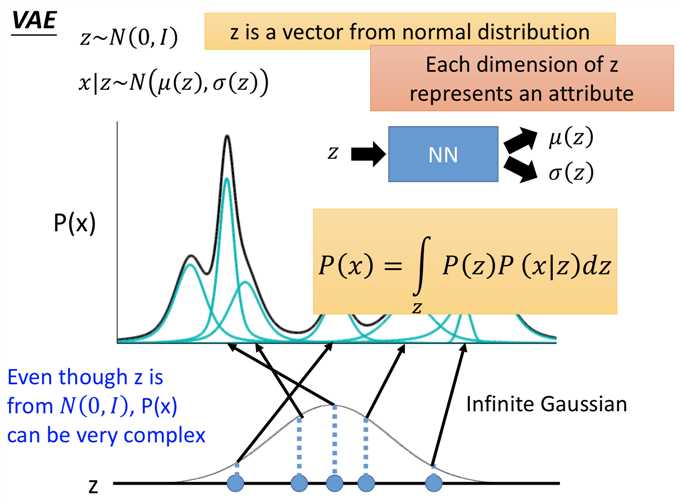
所以在整个 VAE 模型中,关键不是使用 p(z)(先验分布)是正态分布的假设(z服从别的分布也可以),而是假设 p(z | x)(后验分布)是正态分布。
原文:https://www.cnblogs.com/chaojunwang-ml/p/11421454.html