树状数组

定义

  树状数组或者二叉索引树也称作Binary Indexed Tree，又叫做Fenwick树。 它的查询和修改的时间复杂度都是log(n)，空间复杂度则为O(n).

  树状数组可以将线性结构转化成树状结构，从而进行跳跃式扫描，通常使用在高效的计算数列的前缀和，区间和。

实现

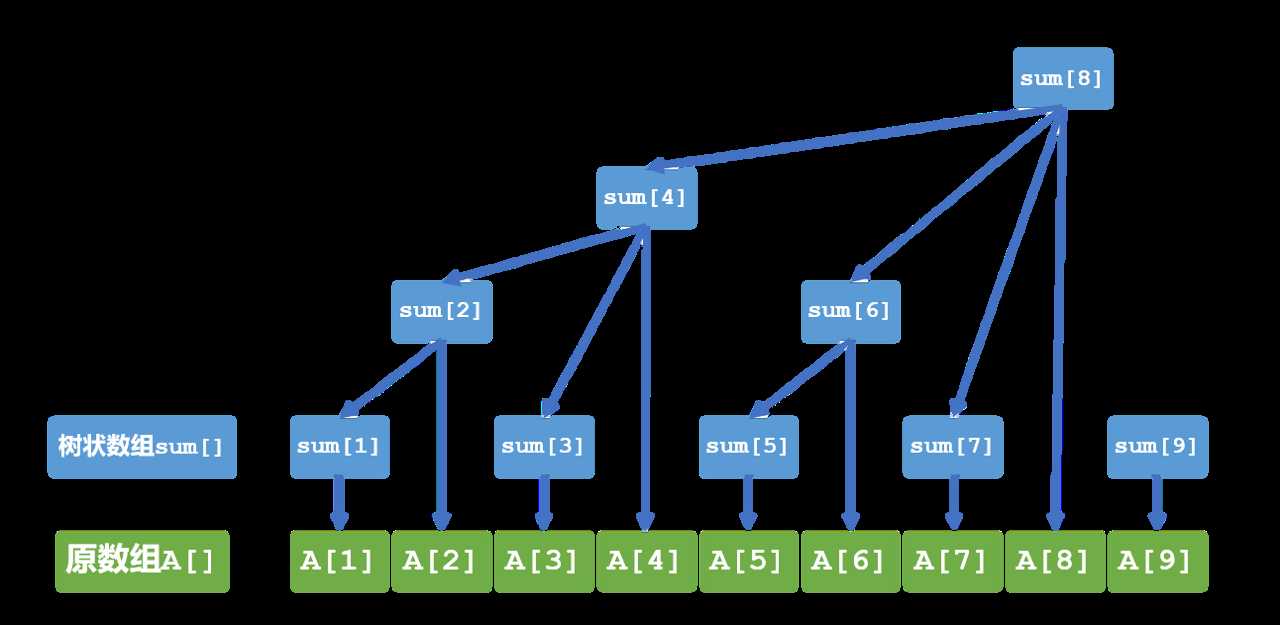
通过图片可以直接得到：

sum1 = A1

sum2 = A1+A2

sum3 = A3

sum4 = A1+A2+A3+A4

sum5 = A5

sum6 = A5+A6

sum7 = A7

sum8 = A1+A2+A3+A4+A5+A6+A7+A8

sum9 = A9

得到//k为i的二进制中从最低位到高位连续零的长度

那么如何求2^k (k为i的二进制中从最低位到高位连续零的长度)

K=i&(-i)

负数的二进制求法为:

①求负数的绝对值的二进制

②反码(0->1，1->0)

③补码(最后一位加1)

例：，所以-5的二进制为1011。

单点更新 + 区间查询

单点更新

更新A[i]时，涉及到的有

例：更新A[5]时，涉及到的有sum[5]，sum[6]，sum[8]

区间查询

令 SUMi 为前i项和，则

例：前七项和为

所以区间[L,R]的和为 

代码

void add(int p, int x)//给位置p增加x
{ 
  while(p <= n) sum[p] += x, p += p & -p;
}
int ask(int p)//求位置p的前缀和
{ 
  int res = 0;
  while(p) res += sum[p], p -= p & -p;
  return res;
}
int range_ask(int l, int r)//区间求和
{ 
  return ask(r) - ask(l - 1);
}

单点查询 + 区间修改 

通过差分实现,原数组为A[i]，令d[i]=A[i]-A[i-1](A[0]=0)

单点查询 

，通过求d[i]的前缀和查询。

区间修改 

当给区间[l,r]加上x的时候，a[l]与前一个元素a[l−1]的差增加了x，a[r+1]与a[r]a[r]的差减少了x。

根据d[i]数组的定义，只需给d[l]加上x,给d[r+1]减去x即可。

代码

void add(int p, int x) //这个函数用来在树状数组中直接修改
{
  while(p <= n) sum[p] += x, p += p & -p;
}
void range_add(int l, int r, int x) //给区间[l, r]加上x
{ 
  add(l, x);
  add(r + 1, -x);
}
int ask(int p) //单点查询
{ 
  int res = 0;
  while(p) res += sum[p], p -= p & -p;
  return res;
}

区间修改 + 区间查询

通过差分实现,原数组为A[i]，令d[i]=A[i]-A[i-1](A[0]=0)

维护两个数组sum1[i]=d[i]，sum2[i]=i*d[i]

区间查询

区间[L,R]的和为=(R+1)*sum1[R]前缀和-sum2[R]前缀和 - L*sum1[L-1]前缀和-sum2[L-1]前缀和。

区间修改

sum1[L]+=x，sum1[R+1]-=x

sum2[L]+=x*L，sum2[R+1]-=x*(R+1)

代码

void add(ll p, ll x)
{
  for(int i = p; i <= n; i += i & -i)
    sum1[i] += x, sum2[i] += x * p;
}
void range_add(ll l, ll r, ll x)
{
  add(l, x);
  add(r + 1, -x);
}
ll ask(ll p)
{
  ll res = 0;
  for(int i = p; i; i -= i & -i)
    res += (p + 1) * sum1[i] - sum2[i];
  return res;
}
ll range_ask(ll l, ll r)
{
  return ask(r) - ask(l - 1);
}

树状数组

原文：https://www.cnblogs.com/VividBinGo/p/11423498.html