09:44:07 2019-08-28
学习
昨天做了 课程要求的 PTA的三道题
基本上涉及了 树的建立 以及树的遍历
今天把昨天 学到的树的遍历 的非递归 实现了一下
写的过程也不是特别顺利 看来 知道代码怎么一回事 和 把代码写出 还是有很大区别的
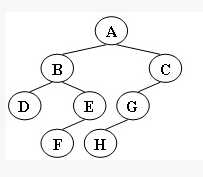
利用 前序中序后序遍历 以及 层序遍历 输出该树

1 #define _CRT_SECURE_NO_WARNINGS //vs中scanf为不安全的函数 要使用 得加上这句话 2 #include<stdio.h> 3 #define Size 10 4 struct TreeNode 5 { 6 char Data; 7 int LeftChild; 8 int RightChild; 9 int times; //为例后序遍历的非递归使用 10 }Tree[10]; 11 int Stack[10]; 12 int STop; //栈顶下标 13 void Push(int Num) 14 { 15 Stack[STop++] = Num; 16 } 17 int Pop() 18 { 19 return Stack[--STop]; 20 } 21 int IsEmpty() 22 { 23 return !STop; 24 } 25 26 int Queue[10]; 27 int Front = 1; 28 int Rear = 0; 29 int QSize; 30 int Succ(int num) //判断是否越界 31 { 32 if (num < Size) 33 return num; 34 else 35 return 0; 36 } 37 void EnQueue(int num) 38 { 39 Rear = Succ(Rear+1); 40 Queue[Rear] =num; 41 QSize++; 42 } 43 int DeQueue() 44 { 45 int num = Queue[Front]; 46 Front = Succ(Front+1); 47 QSize--; 48 return num; 49 } 50 51 //非递归实现遍历 52 //前序中序后序遍历 的非递归做法都是利用栈 因为 前序中序后序的访问顺序是一样的 53 void InOrderTraversal(int Bt); //中序遍历 54 void PreOrderTraversal(int Bt); //先序遍历 55 void PostOrderTraversal(int Bt); //后序遍历 56 57 //层序遍历的做法是利用 队列 58 void LevelOrderTraversal(int Bt); //层序遍历 59 60 void InOrderTraversal(int Bt) 61 { 62 while (Bt!=-1||!IsEmpty()) //空树不输出 如果栈内还有元素 得输出 63 { 64 while (Bt != -1) 65 { 66 Push(Bt); //第一次遇见 67 Bt = Tree[Bt].LeftChild; 68 } 69 if (!IsEmpty()) 70 { 71 int T = Pop(); //第二次遇见 输出 72 printf("%c ", Tree[T].Data); 73 Bt = Tree[T].RightChild; //转向右节点 74 } 75 } 76 } 77 void PreOrderTraversal(int Bt) 78 { 79 while (Bt != -1 || !IsEmpty()) //空树不输出 如果栈内还有元素 得输出 80 { 81 while (Bt != -1) 82 { 83 Push(Bt); //第一次遇见 输出 84 printf("%c ", Tree[Bt].Data); 85 Bt = Tree[Bt].LeftChild; 86 } 87 if (!IsEmpty()) 88 { 89 int T = Pop(); 90 Bt = Tree[T].RightChild; //转向右节点 91 } 92 } 93 } 94 void PostOrderTraversal(int Bt) 95 { 96 while (Bt != -1 || !IsEmpty()) //空树不输出 如果栈内还有元素 得输出 97 { 98 while (Bt != -1) 99 { 100 Push(Bt); //第一次遇见 101 Tree[Bt].times++; 102 Bt = Tree[Bt].LeftChild; 103 } 104 if (!IsEmpty()) 105 { 106 int T = Pop(); 107 if (Tree[T].times == 2) //判断是否第三次遇见 108 printf("%c ", Tree[T].Data); //第三次遇见 输出 109 else 110 { 111 Push(T); 112 Tree[T].times++; 113 Bt = Tree[T].RightChild; //第二次遇见 转向右孩子 114 } 115 } 116 } 117 } 118 119 void LevelOrderTraversal(int Bt) 120 { 121 if (Bt == -1) //空树 122 return; 123 EnQueue(Bt); //首先必须进队 根节点 124 while (QSize) //队列不为空 125 { 126 int T= DeQueue(); 127 printf("%c ", Tree[T].Data); 128 if (Tree[T].LeftChild != -1) EnQueue(Tree[T].LeftChild); 129 if (Tree[T].RightChild != -1)EnQueue(Tree[T].RightChild); 130 } 131 } 132 int Convert(char num) //将字符转换为数字 133 { 134 if (num == ‘-‘) 135 return -1; 136 else 137 return num - ‘0‘; 138 } 139 int BuildTree() //利用 数组建树 140 { 141 int Root=-1; //记录根节点 142 int N=0; 143 int Check[10] = { 0 }; //用来判断根节点的位置 144 scanf("%d\n", &N); 145 for(int i=0;i<N;i++) 146 { 147 char Data, Num1, Num2; 148 scanf("%c %c %c\n", &Data, &Num1, &Num2); 149 Tree[i].Data = Data; 150 Tree[i].LeftChild = Convert(Num1); 151 Tree[i].RightChild = Convert(Num2); 152 if (Tree[i].LeftChild != -1)Check[Tree[i].LeftChild] = 1; 153 if (Tree[i].RightChild != -1)Check[Tree[i].RightChild] = 1; 154 } 155 for (int i = 0; i < N; i++) 156 { 157 if (!Check[i]) 158 Root = i; 159 } 160 return Root; 161 } 162 int main() 163 { 164 int Tree; 165 Tree = BuildTree(); 166 InOrderTraversal(Tree); printf("\n");//中序遍历 167 PreOrderTraversal(Tree); printf("\n"); //先序遍历 168 PostOrderTraversal(Tree); printf("\n"); //后序遍历 169 LevelOrderTraversal(Tree); //层次遍历 170 }
输入数据:
8
A 1 2
B 3 4
C 5 -
D - -
E 6 -
G 7 -
F - -
H - -
输出结果:

结果正确
今天了解了下 二叉搜索树 还学了平衡二叉树(AVL)
然后又被题虐。。
PAT 第9题 判断是否为同一颗 二叉搜索树

1 #define _CRT_SECURE_NO_WARNINGS //vs中scanf为不安全的函数 要使用 得加上这句话 2 #include<stdio.h> 3 #include<malloc.h> 4 typedef struct TNode* BinTree; 5 typedef BinTree Position; 6 struct TNode 7 { 8 int Element; 9 BinTree Left; 10 BinTree Right; 11 }; 12 BinTree Trees[10]; 13 14 BinTree Insert(int Element, BinTree BST) 15 { 16 if (!BST) //BST为空 生成该节点 并且返回 17 { 18 BST = (Position)malloc(sizeof(struct TNode)); 19 BST->Element = Element; BST->Left = NULL; BST->Right = NULL; 20 } 21 else 22 if (Element < BST->Element) 23 BST->Left = Insert(Element, BST->Left); //递归插入左子树 24 else if (BST->Element < Element) 25 BST->Right = Insert(Element, BST->Right); //递归插入右子树 26 return BST; 27 } 28 void MakeTrees(int N, int i) 29 { 30 int num; 31 scanf("%d", &num); 32 Trees[i] = (BinTree)malloc(sizeof(struct TNode)); 33 Trees[i]->Element = num; 34 Trees[i]->Left = Trees[i]->Right = NULL; 35 for (int j = 0; j < N - 1; j++) 36 { 37 scanf("%d", &num); 38 Trees[i] = Insert(num, Trees[i]); 39 } 40 getchar(); 41 } 42 int Charge(BinTree T, BinTree Tree) //判断2个树是否相同 43 { 44 if (T == NULL && Tree == NULL) //空树 一定相同 45 return 1; 46 if (T->Element != Tree->Element) //判断节点处元素是否相同 47 return 0; 48 else 49 return Charge(T->Left, Tree->Left) && Charge(T->Right, Tree->Right); //递归判断2个子树 50 } 51 int main() 52 { 53 int N; 54 int L; 55 scanf("%d", &N); 56 while (N) 57 { 58 scanf("%d\n", &L); 59 for (int i = 0; i <= L; i++) 60 MakeTrees(N, i); 61 for (int i = 1; i <= L; i++) 62 if (Charge(Trees[0], Trees[i])) 63 printf("Yes\n"); 64 else 65 printf("No\n"); 66 scanf("%d", &N); 67 } 68 }
PAT 第10题 找平衡二叉树的根节点

1 #define _CRT_SECURE_NO_WARNINGS //vs中scanf为不安全的函数 要使用 得加上这句话 2 #include<stdio.h> 3 #include<malloc.h> 4 typedef struct TNode* BinTree; 5 typedef BinTree Position; 6 struct TNode 7 { 8 int Element; 9 BinTree Left; 10 BinTree Right; 11 int Heigth; //高度 12 }; 13 int GetHeight(BinTree T) 14 { 15 if (!T) 16 return -1; 17 else 18 return T->Heigth; 19 } 20 21 int Max(int a, int b) 22 { 23 return (a > b) ? a : b; 24 } 25 BinTree NewNode(int Element) 26 { 27 BinTree T = (BinTree)malloc(sizeof(struct TNode)); 28 T->Element = Element; 29 T->Left = NULL; 30 T->Right = NULL; 31 T->Heigth = 0; 32 return T; 33 } 34 BinTree SingleLeftRotation(BinTree T) 35 { 36 BinTree TL = T->Left; 37 T->Left = TL->Right; 38 TL->Right = T; 39 T->Heigth = Max(GetHeight(T->Left), GetHeight(T->Right)) + 1; 40 TL->Heigth = Max(GetHeight(TL->Left),T->Heigth)+1; 41 return TL; 42 } 43 BinTree SingleRightRotation(BinTree T) 44 { 45 BinTree TR = T->Right; 46 T->Right = TR->Left; 47 TR->Left = T; 48 T->Heigth = Max(GetHeight(T->Left),GetHeight(T->Right))+1; 49 TR->Heigth =Max(GetHeight(TR->Right),T->Heigth)+1; 50 return TR; 51 } 52 BinTree DoubleLeftRightRotation(BinTree T) 53 { //先做一次右单旋 再做一次左单旋 54 T->Left = SingleRightRotation(T->Left); 55 return SingleLeftRotation(T); 56 } 57 BinTree DoubleRightLeftRotation(BinTree T) 58 {//先做一次左旋 再做一次右旋 59 T->Right = SingleLeftRotation(T->Right); 60 return SingleRightRotation(T); 61 } 62 BinTree Insert(int Element, BinTree BST) 63 { 64 if (!BST) //BST为空 生成该节点 并且返回 65 BST = NewNode(Element); 66 else 67 if (Element < BST->Element) 68 { 69 BST->Left = Insert(Element, BST->Left); //递归插入左子树 70 if (GetHeight(BST->Left) - GetHeight(BST->Right) == 2) //判断是否需要进行旋转 71 if (Element < BST->Left->Element) //左单旋 72 BST=SingleLeftRotation(BST); 73 else 74 BST=DoubleLeftRightRotation(BST); //左-右双旋 75 } 76 else if (BST->Element < Element) 77 { 78 BST->Right = Insert(Element, BST->Right); //递归插入右子树 79 if (GetHeight(BST->Left) - GetHeight(BST->Right) == -2) 80 if (Element > BST->Right->Element) //右单旋 81 BST=SingleRightRotation(BST); 82 else 83 BST=DoubleRightLeftRotation(BST); //右-左双旋 84 } 85 BST->Heigth = Max(GetHeight(BST->Left), GetHeight(BST->Right)) + 1; 86 return BST; 87 } 88 BinTree MakeTree() 89 { 90 int N; 91 scanf("%d",&N); 92 int num; 93 scanf("%d", &num); 94 BinTree T = NewNode(num); 95 for (int i = 1; i < N; i++) 96 { 97 scanf("%d", &num); 98 T=Insert(num, T); 99 } 100 return T; 101 } 102 int main() 103 { 104 BinTree Root = MakeTree(); 105 printf("%d", Root->Element); 106 }
首先 我发现了 我刚开始数据输入就不对 格式什么都不匹配 再者 也想不出什么算法来。。。
原文:https://www.cnblogs.com/57one/p/11423218.html