DIjkstra算法

DIjkstra算法

　　　一.算法思想

　　　　　　步骤如下：

　　　　　　1、选取一个起点s，设置一个int型数组（此处使用数组d）表示起点到各个点的最短距离，设置一个bool型数组（此处使用数组vis）表示每个点是否访问过

　　　　　　2、让起点到各个点的距离变为INF无限大（起点到自己的距离应该为0）

　　　　　　3、重复一下过程n次（n为顶点个数）

　　　　　　{

　　　　　　　　1、在所有未访问的节点中选取到达其最短路最短的那一个（其实就是找一个d数组中最小并且为访问的）

　　　　　　　　2、把它标记为访问过

　　　　　　　　3、把所有与它相连的点更新

　　　　　　}

　　　　　eg.要求在下图中找到从a到b的最短路

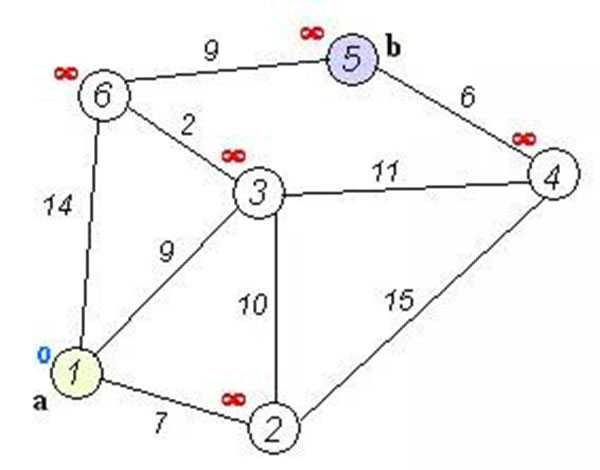
　　　　　　①：选取1作为起点，现在d数组是{0,INF,INF,INF,INF,INF}

　　　　　　②：通过1把与其相邻的点更新——————d数组变为{0,7,9,INF,INF,14}

　　　　　　③：选取下一个点——————2

　　　　　　④：通过2把与其相邻的点更新——————d数组变为{0,7,9,22,INF,14}

　　　　　　⑤：选取下一个点——————3

　　　　　　⑥：通过3把与其相邻的点更新——————d数组变为{0,7,9,20,INF,11}

　　　　　　⑦：选取下一个点——————6

　　　　　　⑧：通过6把与其相邻的点更新——————d数组变为{0,7,9,20,20,11}

　　　　　　⑨：选取下一个点——————4

　　　　　　⑩：通过4把与其相邻的点更新——————d数组变为{0,7,9,20,20,11}

　　　　　　 shi‘yi：选取下一个点——————4

　　　　　　⑩：通过4把与其相邻的点更新——————d数组变为{0,7,9,20,20,11}

　　　　　　…………

　　　　　　于是，Dijkstra的代码就可以很轻易地得出：

void Dijkstra(int s)
{
    memset(vis,false,sizeof(vis));
    for(int i=2;i<=n;i++)
    {
        d[i]=INF;//初始化 
    }
    d[s]=0;
    for(int i=1;i<=n;i++)
    {
        int pos=-1;
        int MIN=INF;
        for(int j=1;j<=n;j++)
        {
            if(d[j]<MIN && vis[j]==false)//找出下一个要访问的点 
            {
                MIN=d[j];
                pos=j;
            }
        }
        if(pos==-1)//如果找不到就证明剩余的点与此点不连接 
        {
            break;
        }
        vis[pos]=true;
        for(int j=0;j<G[pos].size();j++)
        {
            int v=G[pos][j].v;
            if(G[pos][j].w+d[pos]<d[v] && vis[v]==false)
            {
                d[v]=G[pos][j].w+d[pos];//更新每一个点 
            }
        }
    }
}

DIjkstra算法

原文：https://www.cnblogs.com/qlnj/p/11432653.html