题目:
InputThere are TT tests (T≤50T≤50). Each test contains one integer NN. 1≤N≤1000000000 (109)1≤N≤1000000000 (109). Process till the end of input.OutputFor each test, output the answer mod 1000000007 (109+7109+7) in one line.Sample Input
4 7 10
Sample Output
3 5 15
解题报告:这个题目一开始可以根据手算推导出前边的数,然后根据oeis可以快速找到该序列的规律
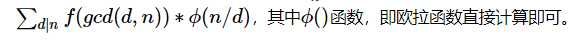
这个,咱们直接去求解n的所有因子d,eluer(n/d)*(f(d+1)+f(d-1)),所有结果求和,然后除以n,这个时候需要使用逆元。
ac代码:
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long ll;
int T;
ll n;
const ll mod=1e9+7;
const int maxn=1e5+1000;
int f[maxn];
int phi[maxn];
void db_f()
{
f[1]=1;
f[2]=3;
for(int i=3;i<maxn;i++)
f[i]=(f[i-1]+f[i-2])%mod;
}
ll ksm(ll a,ll b)
{
ll res=1;
a%=mod;
while(b)
{
if(b&1)
res=(res*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return res;
}
ll eluer(ll n)
{
ll res=n;
for(int i=2;i*i<=n;i++)
{
if(n%i==0)
res=res/i*(i-1);
while(n%i==0)
n/=i;
}
if(n>1)
res=res/n*(n-1);
return res;
}
struct Mat{
ll a[5][5];
};
Mat mat_mul(Mat a,Mat b)
{
Mat c;
for(int i=0;i<2;i++)
{
for(int j=0;j<2;j++)
{
c.a[i][j]=0;
for(int k=0;k<2;k++)
{
c.a[i][j]+=a.a[i][k]*b.a[k][j];
c.a[i][j]%=mod;
}
}
}
return c;
}
Mat mat_ksm(Mat a,ll n)
{
Mat res;
res.a[0][0]=res.a[1][1]=1;
res.a[0][1]=res.a[1][0]=0;
while(n)
{
if(n&1) res=mat_mul(res,a);
a=mat_mul(a,a);
n>>=1;
}
return res;
}
ll get_f(int n)
{
if(n<100000)
return f[n];
Mat a;
a.a[0][0]=1;
a.a[0][1]=1;
a.a[1][0]=1;
a.a[1][1]=0;
a=mat_ksm(a,n-2);
return 3*a.a[0][0]+a.a[0][1];
}
int main()
{
db_f();
while(scanf("%d",&n)!=EOF)
{
if(n==1)
{
printf("2\n");
continue;
}
ll ans=0;
for(ll i=1;i*i<=n;i++)
{
if(n%i==0)
{
ll tmp=(get_f(i)%mod*eluer(n/i)%mod);
ans=(ans+tmp)%mod;
if(i*i!=n)
{
ll j=n/i;
tmp=get_f(j)%mod*eluer(n/j)%mod;
ans=(ans+tmp)%mod;
}
}
}
printf("%lld\n",(ans*ksm(n,mod-2)%mod)%mod);
}
}
Different Circle Permutation (HDU - 5868) (欧拉函数+矩阵快速幂)
原文:https://www.cnblogs.com/Spring-Onion/p/11434493.html