斐波那契数列,是软件人的一位老朋友了,今天我们就来回顾一下教科书上的写法以及这种写法性能上的弊端?有没有更好的写法?
1.首先,教科书的问法是求斐波那契数列的第N项;写一个函数,输入n,求出第N项目。数列定义如下: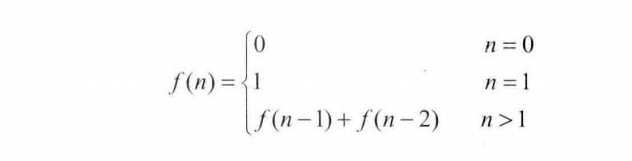
于是接下来就会引申出递归函数的用法,以及代码(c#)实例:
1 /// <summary> 2 /// 斐波那契数列低级写法 3 /// </summary> 4 /// <param name="targetNumber">输入的目标值</param> 5 /// <returns></returns> 6 public int Fibonacci(int targetNumber) 7 { 8 //算法开始 9 if (targetNumber <= 0) 10 return 0; 11 if (targetNumber == 1) 12 return 1; 13 return Fibonacci(targetNumber - 1) + Fibonacci(targetNumber - 2); 14 }
得出结果并没有任何问题。但是这种写法可靠吗?是我们想要的吗?
我们来分析一下为什么这种写法会有很严重的效率问题。
首先我们求解f(10),就需要得到f(9)与f(8),想要求解f(9),势必要求出f(8)与f(7),大家看到了吗?这种重复求解的关系是很糟糕的,并且会随着节点数会随着n的增大而急剧增大。如如下依赖关系图所示: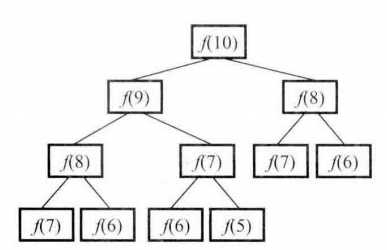
那我们有没有更好的写法呢?当然有,因为递归与循环本来就是一家人!如下代码(C#)实例:
/// <summary> /// 斐波那契数列高级写法 避免重复计算 /// </summary> /// <param name="targerNumber">输入的目标值</param> /// <returns></returns> public int FibonacciPro(int targetNumber) { Stopwatch sw = new Stopwatch(); sw.Start(); //算法开始 int[] arrayBase = {0, 1}; if (targetNumber < 2) return arrayBase[targetNumber]; int fibNumberOne = 1; int fibNumberTwo = 0; int fibCurrentNumber = 0; for (int i = 2; i <= targetNumber; ++i) { fibCurrentNumber = fibNumberOne + fibNumberTwo; fibNumberTwo = fibNumberOne; fibNumberOne = fibCurrentNumber; } sw.Stop(); TimeSpan ts = sw.Elapsed; Console.WriteLine("Para is {0},Datatime Costed For Shuffle Function is {1}ms", targetNumber, ts.TotalMilliseconds); return fibCurrentNumber; }
写完了之后我们来看一下性能方面到底是不是节约了很多?
首先,当参数N为10的时候: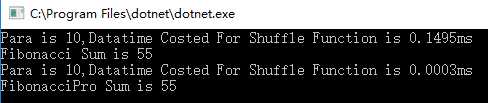
这里已经可以初步看到效率有了明显的提升!
当参数N为30的时候,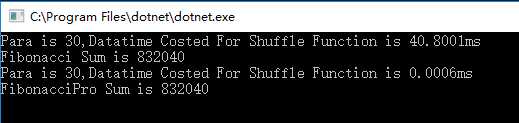
这里的性能已经有了天翻地覆的差别!
除此之外,第一种方式的递归还有可能引起严重的栈溢出,每一次调用函数都会在内存栈种分配空间,而每个进程的栈容量是有限的,若第一种解法N参数为5000,则运行时候会出错,但是第二种解法则能得到正确结果。
原文:https://www.cnblogs.com/zangjiapei/p/11434596.html