1.归并排序 O(nlogn) stable
#include <iostream> #include <vector> using namespace std; void merge(vector<int>& arr, int l, int mid, int r){ int n1 = mid - l + 1, n2 = r - mid; vector<int> left(n1); vector<int> right(n2); for(int i = 0; i < n1; ++i) left[i] = arr[l + i]; for(int i = 0; i < n2; ++i) right[i] = arr[mid + 1 + i]; int i = 0, j = 0, k = l; while(i < n1 && j < n2){ if(left[i] <= right[j]) arr[k++] = left[i++]; else arr[k++] = right[j++]; } while(i < n1) arr[k++] = left[i++]; while(j < n2) arr[k++] = right[j++]; } void mergeSort(vector<int>& arr, int l, int r){ if(l < r){ int mid = (l + r) / 2; mergeSort(arr, l, mid); mergeSort(arr, mid + 1, r); merge(arr, l, mid, r); } } int main(){ vector<int> input = {3, 4, 6, 1, 9, 5, 2, 7, 0, 8}; mergeSort(input, 0, input.size() - 1); for(int i : input) cout << i << " "; return 0; }
2.数组中逆序对个数Count Inversions
#include <iostream> #include <vector> using namespace std; int merge(vector<int>& arr, int l, int mid, int r); int mergeSort(vector<int>& arr, int l, int r){ int invCount = 0; if(l < r){ int mid = (l + r) / 2; invCount = mergeSort(arr, l, mid); invCount += mergeSort(arr, mid + 1, r); invCount += merge(arr, l, mid, r); } return invCount; } int merge(vector<int>& arr, int l, int mid, int r){ int n1 = mid - l + 1, n2 = r - mid; vector<int> left(n1); vector<int> right(n2); for(int i = 0; i < n1; ++i) left[i] = arr[l + i]; for(int i = 0; i < n2; ++i) right[i] = arr[mid + 1 + i]; int i = 0, j = 0, k = l; int invCount = 0; while(i < n1 && j < n2){ if(left[i] > right[j]){ invCount += mid - i + 1; arr[k++] = right[j++]; } else arr[k++] = left[i++]; } while(i < n1) arr[k++] = left[i++]; while(j < n2) arr[k++] = right[j++]; return invCount; } int main(){ vector<int> input = {1, 3, 5, 2, 4}; int ans = mergeSort(input, 0, input.size() - 1); for(int i : input) cout << i << " "; cout << endl; cout << ans; return 0; }
3.Leetcode 493 Reverse Pairs
Given an array nums, we call (i, j) an important reverse pair if i < j and nums[i] > 2 * nums[j]. You need to return the number of important reverse pairs in the given array.
class Solution { public: vector<int> helper; int reversePairs(vector<int>& nums) { helper.resize(nums.size()); return mergeSort(nums, 0, nums.size() - 1); } int mergeSort(vector<int>& nums, int s, int e){ if(s >= e) return 0; int mid = s + (e - s) / 2; int cnt = mergeSort(nums, s, mid) + mergeSort(nums, mid + 1, e); for(int i = s, j = mid + 1; i <= mid; ++i){ while(j <= e && nums[i] / 2.0 > nums[j]) j++; cnt += j - (mid + 1); } merge(nums, s, mid, e); return cnt; } void merge(vector<int>& nums, int s, int mid, int e){ for(int i = s; i <= e; ++i) helper[i] = nums[i]; int p1 = s; int p2 = mid + 1; int i = s; while(p1 <= mid || p2 <= e){ //注意这个merge的逻辑 if(p1 > mid || p2 <= e && helper[p1] >= helper[p2]) nums[i++] = helper[p2++]; else nums[i++] = helper[p1++]; } } };
4.Leetcode 315 Count of Smaller Numbers After self
You are given an integer array nums and you have to return a new counts array. The counts array has the porperty where counts[i] is the number o f smaller elements to the right of nums[i].
class Solution { public: unordered_map<int, int> count; vector<int> helper; vector<int> countSmaller(vector<int>& nums) { vector<int> numsCopy = nums; helper.resize(nums.size()); vector<int> res(nums.size()); mergeSort(nums, 0, nums.size() - 1); for(int i = 0; i < nums.size(); ++i){ res[i] = count[numsCopy[i]]; } return res; } void mergeSort(vector<int>& nums, int s, int e){ if(s < e){ int mid = s + (e - s) / 2; mergeSort(nums, s, mid); mergeSort(nums, mid + 1, e); for(int i = s, j = mid + 1; i <= mid; ++i){ while(j <= e && nums[i] > nums[j]) j++; count[nums[i]] += j - (mid + 1); } merge(nums, s, mid, e); } } void merge(vector<int>& nums, int s, int mid, int e){ for(int i = s; i <= e; ++i) helper[i] = nums[i]; int p1 = s; int p2 = mid + 1; int i = s; while(p1 <= mid || p2 <= e){ if(p1 > mid || p2 <= e && helper[p1] >= helper[p2]) nums[i++] = helper[p2++]; else nums[i++] = helper[p1++]; } } };
5.Count of Range Sum
Given an interger array nums, return the number of range sums that lie in [lower, upper] inclusive. Range sum S(i, j) is defined as the sum of the elements in nums between indices i and j (i <= j), inclusive.
Note: A naive algorithm of $O(n_2)$ is trivial. You MUST do better than that.
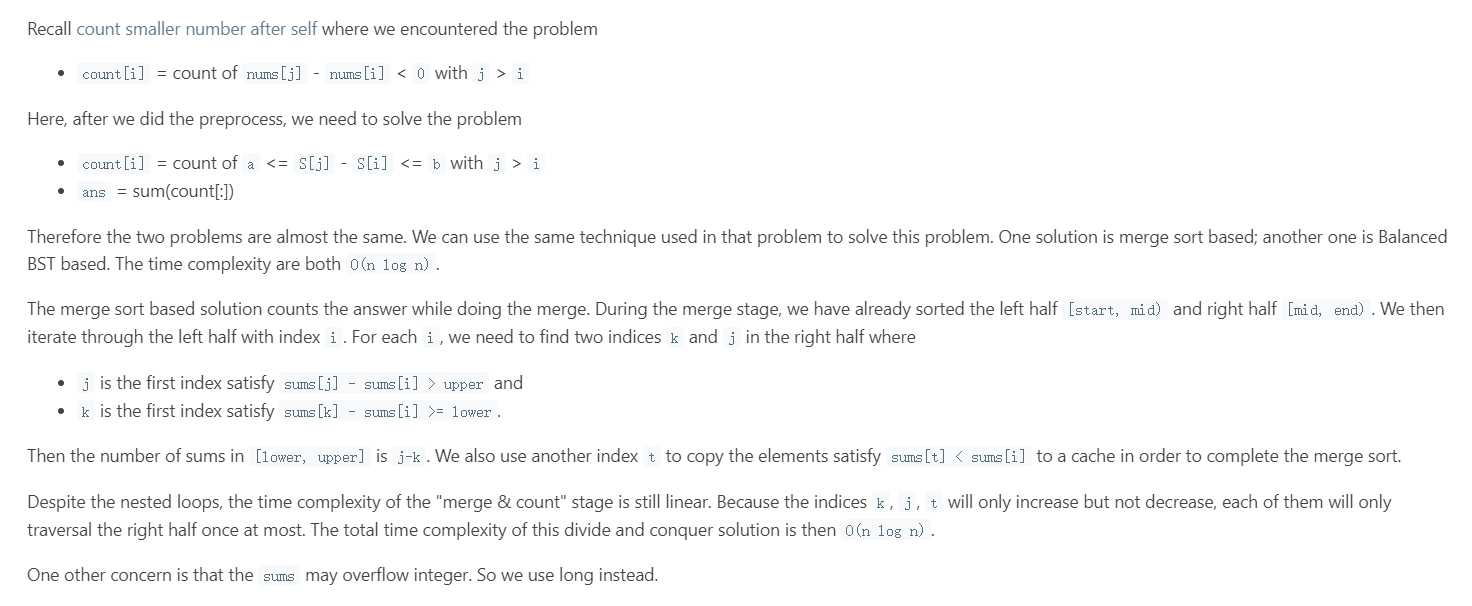
class Solution { public: int countRangeSum(vector<int>& nums, int lower, int upper) { int size = nums.size(); if(size == 0) return 0; vector<long> sums(size + 1, 0); for(int i = 0; i < size; ++i) sums[i + 1] = sums[i] + nums[i]; return help(sums, 0, size + 1, lower, upper); } int help(vector<long>& sums, int start, int end, int lower, int upper){ if(end - start <= 1) return 0; int mid = (start + end) / 2; int cnt = help(sums, start, mid, lower, upper) + help(sums, mid, end, lower, upper); int m = mid, n = mid, t = mid, len = 0; vector<long> cache(end - start, 0); for(int i = start, s = 0; i < mid; ++i, ++s){ while(m < end && sums[m] - sums[i] < lower) ++m; while(n < end && sums[n] - sums[i] <= upper) ++n; cnt += n - m; while(t < end && sums[t] < sums[i]) cache[s++] = sums[t++]; cache[s] = sums[i]; len = s; } for(int i = 0; i <= len; ++i) sums[start + i] = cache[i]; return cnt; } };
原文:https://www.cnblogs.com/betaa/p/11438599.html