题解 P5530 [BalticOI 2002]双调路径

P5530 [BalticOI 2002]双调路径

输入样例：
4 5 1 4
2 1 2 1
3 4 3 1
2 3 1 2
3 1 1 4
2 4 2 4

样例如下图

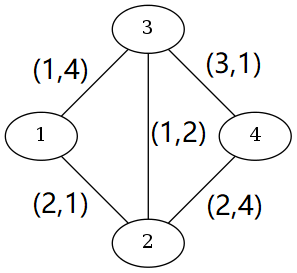
样例说明：

从1到4有4条路径。为1→2→4(费用为4,时间为5) ,1→3→4(费用为4,时间为5) ,1→2→3→4(费用为6,时间为4) ,1→3→2→4(费用为4,时间为10)。 1→3→4和1→2→4比1→3→2→4更好。有两种最佳路径:费用为4 ,时间为5(1→2→4和1→3→4)和费用为6,时间为4 (1→2→3→4)。

分析

最短路的边有两种权值，所以考虑在每个节点增加一维状态，d【i】【j】：到达节点i且费用为j时所用最少时间，则d【v】【j】=min{d【u】【j-cost（u，v）】}+time（u，v）

用SPFA即可， 533ms / 6.12MB，#8#9TLE，86分

#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;
#define R register
struct edge {
    int v,w,t,h;
} e[610];
int h[110],d[110][10100],cnt,mn;
int u,v,w,n,m,S,T;
bool vis[110][10100];//第二维记得开大一些

inline void add(int u,int v,int w,int t) {
    e[++cnt]=(edge) {v,w,t,h[u]},h[u]=cnt;
}

queue<pair<int,int> >q;//二维记录节点u和所用cost
inline void spfa() {
    memset(d,0x3f,sizeof d);
    mn=99999999;
    q.push(make_pair(S,d[S][0]=0)),vis[S][0]=1;
    while(!q.empty()) {
        u=q.front().first,w=q.front().second;
        vis[u][w]=0,q.pop();
        for (R int i=h[u],_w; i; i=e[i].h)
            if ((_w=w+e[i].w)<=10010) {//w是到达u的cost，_w是由u到达v所用cost，_w超出100*100直接舍去
                if (d[v=e[i].v][_w]>d[u][w]+e[i].t) {//同样的cost所用time是否比原来更少
                    d[v][_w]=d[u][w]+e[i].t;
                    if(!vis[v][_w]) q.push(make_pair(v,_w)),vis[v][_w]=1;
                }
            }
    }
}

int main() {
    scanf("%d%d%d%d",&n,&m,&S,&T);
    for (R int t; m; m--)
        scanf("%d%d%d%d",&u,&v,&w,&t),add(u,v,w,t),add(v,u,w,t);
    spfa();

    cnt=0;
    for (R int i=0; i<=10000; i++)
        if(d[T][i]<mn) mn=d[T][i],cnt++;//cost逐渐增长，那么time只有小于其他的time才能算“最小路径”
    printf("%d",cnt);
}

优化

不难想到，对于d【i】【j】，如果有k（k<j）且d【i】【k】<d【i】【j】（到达i所用cost和time都更少），那么d【i】【j】也就没必要更新了。所以加入剪枝：用树状数组维护d【i】【0~j】的最小值，只有d【i】【j】<最小值才更新

实际效率提高不少， 93ms / 9.93MB，AC代码：

#include<cstdio>
#include<queue>
#include<cstring>
#include<iostream>
using namespace std;
#define R register
struct edge {
    int v,w,t,h;
} e[610];
int h[110],d[110][10100],tr[110][10100],cnt,mn;
int u,v,w,n,m,S,T;
bool vis[110][10100];

inline void add(int u,int v,int w,int t) {
    e[++cnt]=(edge) {v,w,t,h[u]},h[u]=cnt;
}

//用val更新d【x】【0~y】最小值    
inline void upd(int x,int y,int val){
    for (y++;y<10100;y+=y&-y) tr[x][y]=min(tr[x][y],val);
}//树状数组下标不能为0，所以y++

//查询d【x】【0~y】最小值
inline int qry(int x,int y){
    int ans=1e7;
    for (y++;y;y-=y&-y) ans=min(tr[x][y],ans);
    return ans;
}

queue<pair<int,int> >q;
inline void spfa() {
    memset(d,0x3f,sizeof d);
    memset(tr,0x3f,sizeof d);//别忘了初始化
    q.push(make_pair(S,d[S][0]=0)),vis[S][0]=1;
    upd(S,0,0);
    while(!q.empty()) {
        u=q.front().first,w=q.front().second;
        vis[u][w]=0,q.pop();
        for (R int i=h[u],_w; i; i=e[i].h)
                if (qry(v=e[i].v,_w=w+e[i].w)>d[u][w]+e[i].t) {//只有d【i】【j】<最小值才更新
                    d[v][_w]=d[u][w]+e[i].t;
                    upd(v,_w,d[v][_w]);//更新最小值
                    if(!vis[v][_w]) q.push(make_pair(v,_w)),vis[v][_w]=1;
                }
    }
}

int main() {
    scanf("%d%d%d%d",&n,&m,&S,&T);
    for (R int t; m; m--)
        scanf("%d%d%d%d",&u,&v,&w,&t),add(u,v,w,t),add(v,u,w,t);
    spfa();

    cnt=0,mn=99999999;
    for (R int i=0; i<=10000; i++)
        if(d[T][i]<mn) mn=d[T][i],cnt++;
    printf("%d",cnt);
}

题解 P5530 [BalticOI 2002]双调路径

原文：https://www.cnblogs.com/Randolph68706/p/11439741.html