
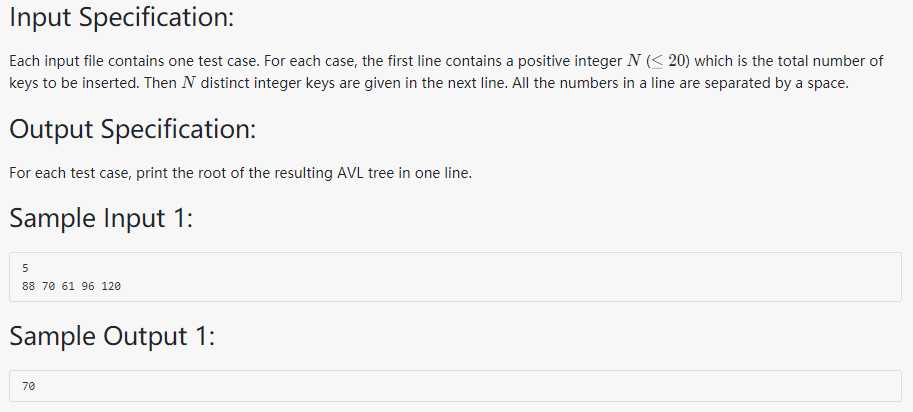
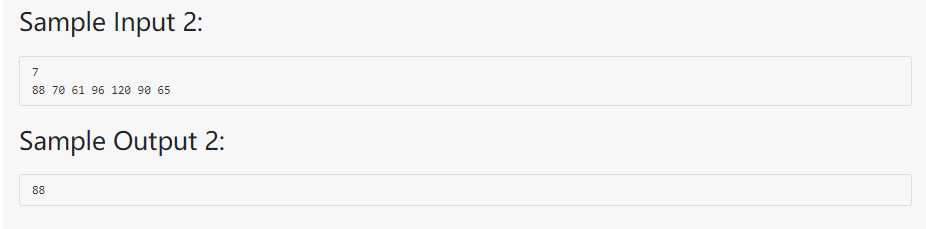
这道题主要为了考察对AVL树的插入与旋转等操作。
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
struct AVLNode
{
int Data; //节点数据
struct AVLNode* Left; //指向左子树
struct AVLNode* Right; //指向右子树
int Height; //树高
};
int Max(int a,int b)
{
return a > b ? a : b;
}
//返回树的高度
int GetH(struct AVLNode* T)
{
if (T)
{
return T->Height;
}
else
{
return -1;
}
}
//右单旋 RR
struct AVLNode* RR(struct AVLNode* A)
{
struct AVLNode* B; //旋转后的根节点
B = A->Right;
A->Right = B->Left;
B->Left = A;
//更新树的高度
A->Height = Max(GetH(A->Left),GetH(A->Right)) + 1;
B->Height = Max(GetH(B->Left),A->Height) + 1;
return B;
}
struct AVLNode* LL(struct AVLNode* A)
{
struct AVLNode* B;
B = A->Left;
A->Left = B->Right;
B->Right = A;
A->Height = Max(GetH(A->Left),GetH(A->Right)) + 1;
B->Height = Max(GetH(B->Left), A->Height) + 1;
return B;
}
//LR双旋直接实现
struct AVLNode* LR(struct AVLNode* A)
{
struct AVLNode* B, *C;
B = A->Left;
C = B->Right;
B->Right = C->Left;
A->Left = C->Right;
C->Left = B;
C->Right = A;
B->Height = Max(GetH(B->Left), GetH(B->Right)) + 1;
A->Height = Max(GetH(A->Left),GetH(A->Right)) + 1;
C->Height = Max(B->Height,A->Height) + 1;
return C;
}
//RL双旋直接实现
struct AVLNode* RL(struct AVLNode* A)
{
struct AVLNode* B, *C;
B = A->Right;
C = B->Left;
B->Left = C->Right;
A->Right = C->Left;
C->Left = A;
C->Right = B;
B->Height = Max(GetH(B->Left), GetH(B->Right)) + 1;
A->Height = Max(GetH(A->Left), GetH(A->Right)) + 1;
C->Height = Max(A->Height, B->Height) + 1;
return C;
}
//作用:将x插入AVL树T中,并且返回调整后的AVL树
struct AVLNode* Insert(struct AVLNode* T, int x)
{
if (!T)
{
//若插入空树 则新建包含一个节点的树
T = (struct AVLNode*)malloc(sizeof(struct AVLNode));
T->Data = x;
T->Left = NULL;
T->Right = NULL;
T->Height = 0;
}
else if (x < T->Data)
{
//插入T的左子树
T->Left = Insert(T->Left, x);
//如果需要左旋
if (GetH(T->Left) - GetH(T->Right) == 2)
{
if (x < T->Left->Data)
{
//左单旋
T = LL(T);
}
else
{
//左右双旋
T = LR(T);
}
}
}
else if (x > T->Data)
{
//插入T的右子树
//插入T的左子树
T->Right = Insert(T->Right, x);
//如果需要左旋
if (GetH(T->Left) - GetH(T->Right) == -2)
{
if (x > T->Right->Data)
{
//右单旋
T = RR(T);
}
else
{
//右左双旋
T = RL(T);
}
}
}//else if 插入右子树结束
//更新树高
T->Height = Max(GetH(T->Left),GetH(T->Right)) + 1;
return T;
}
int main()
{
int N;
int K;
struct AVLNode* T = NULL;
scanf("%d",&N);
for (int i = 0; i< N;i++)
{
scanf("%d",&K);
T = Insert(T, K);
}
printf("%d",T->Data);
//system("pause");
return 0;
}原文:https://www.cnblogs.com/Manual-Linux/p/11439770.html