二阶偏导数矩阵也就所谓的赫氏矩阵(Hessian matrix).
一元函数就是二阶导,多元函数就是二阶偏导组成的矩阵.
求向量函数最小值时用的,矩阵正定是最小值存在的充分条件。
经济学中常常遇到求最优的问题,目标函数是多元非线性函数的极值问题尚无一般的求解方法,但判定局部极小值的方法是有的,就是用hessian矩阵,
在x0点上,hessian矩阵是负定的,且各分量的一阶偏导数为0,则x0为极大值点.
在x0点上,hessian矩阵是正定的,且各分量的一阶偏导数为0,则x0为极小值点.
矩阵是负定的充要条件是各个特征值均为负数.
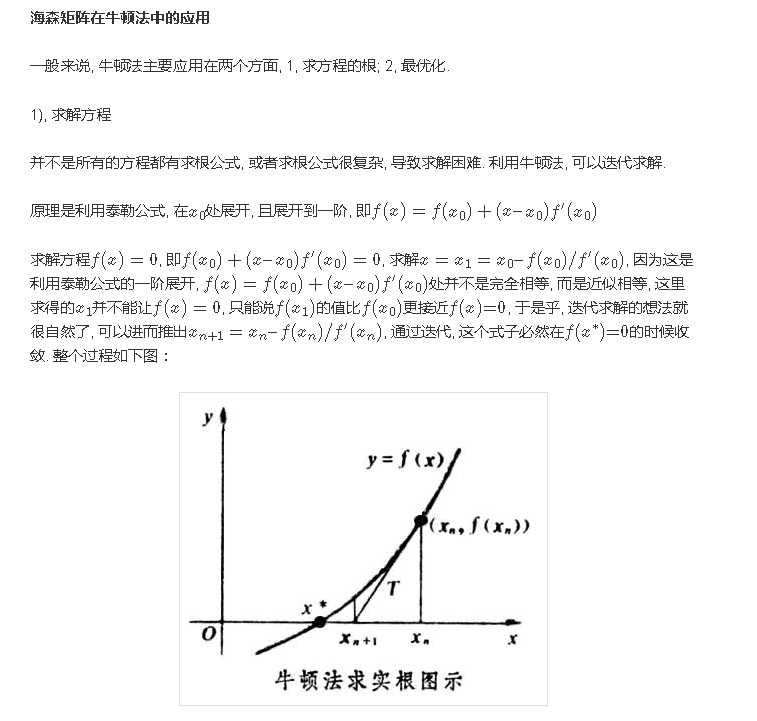
矩阵是正定的充要条件是各个特征值均为正数.
设n多元实函数  在点
在点 的邻域内有二阶连续偏导,若有:
的邻域内有二阶连续偏导,若有:

且

则:
当A正定矩阵时,  在
在 处是极小值
处是极小值
当A负定矩阵时, 在
在 处是极大值
处是极大值
当A不定矩阵时,  不是极值点
不是极值点
当A为半正定矩阵或半负定矩阵时, 是“可疑”极值点,尚需要利用其他方法来判定。
是“可疑”极值点,尚需要利用其他方法来判定。


2), 最优化
在最优化的问题中, 线性最优化至少可以使用单纯形法(或称不动点算法)求解, 但对于非线性优化问题, 牛顿法提供了一种求解的办法. 假设任务是优化一个目标函数ff, 求函数ff的极大极小问题, 可以转化为求解函数ff的导数f′=0f′=0的问题, 这样求可以把优化问题看成方程求解问题(f′=0f′=0). 剩下的问题就和第一部分提到的牛顿法求解很相似了.
这次为了求解f′=0f′=0的根, 把f(x)f(x)的泰勒展开, 展开到2阶形式:


原文:https://www.cnblogs.com/rswss/p/11440190.html