除了之前说的从空间滤波器中获得频率域滤波器,还可以从频率域中直接生成滤波器,这些滤波器被规定为距滤波器中心点的距离不同的函数。可以创建一个用于实现频率滤波器的网格数组,最主要的是需要计算任何点到频率矩形中一个指定点的距离函数,FFT(快速傅里叶)算法是假设变换的原点位于频率矩形的左上角,因此需要将原点平移到频率矩形的中心,用fftshift。网格数组如下:
%(频域滤波函数) 提供了距离计算及其所需的网格数组 function [U,V] = dftuv(M,N) u=0:(M-1); v=0:(N-1); idx = find(u>M/2); u(idx) = u(idx)-M; idy=find(v>N/2); v(idy)=v(idy)- N; [V,U] = meshgrid(v,u); end
常见的频率域低通滤波器有三个,理想低通滤波器(ILPF),巴特沃斯低通滤波器(BLPF),高斯低通滤波器(GLPF)。
1)理想低通滤波器的传递函数如下:
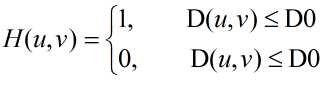
其中,D0为正数,D(u,v)为点(u,v)到滤波器中心的距离,满足D(u,v)=D0的点的轨迹为一个圆。如果用滤波器乘以一幅图像的傅里叶变换,我们会看到一个理想滤波器会切断(乘以0)该圆之外的所有F(u,v)分量,而保留圆上和圆内的所有分量不变(乘以1)。
可以用之前的mesh将滤波器显示出来:


2)n阶巴特沃斯低通滤波器,在距离滤波器中心D0处具有截止频率,传递函数为:
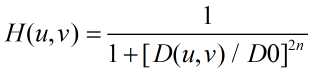
与理想低通滤波器不同的是,巴特沃斯低通滤波器的传递函数在D0点并没有一个尖锐的不连续,对于具有平滑传递函数的滤波器,通常将截止频率轨迹定义在H(u,v)降低为其最大值的一个指定的比例的点处。用mesh同样可以将该滤波器显示出来:
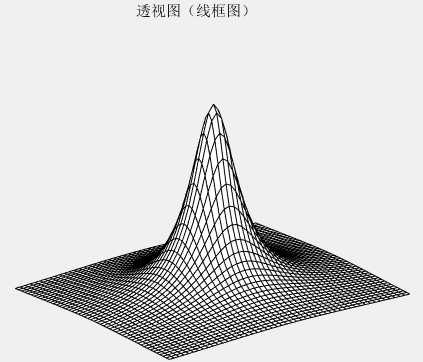

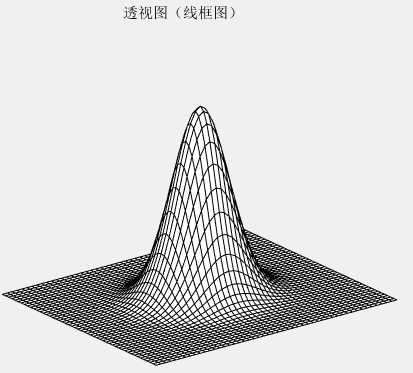
3)高斯低通滤波器的传递函数如下:
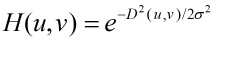
其中,![]() 为标准差。该滤波器可以用mesh显示出来
为标准差。该滤波器可以用mesh显示出来

4)低通滤波器的例子
用高斯低通滤波器对一幅500*500的图像进行滤波,效果如下:

该例子的代码如下:
%用高斯低通滤波器进行滤波 f=imread(‘G:\数字图像处理(冈萨雷斯)\DIP3E_CH04_Original_Images\DIP3E_Original_Images_CH04\Fig0441(a)(characters_test_pattern).tif‘); subplot(221);imshow(f); title(‘原图‘) f = im2double(f); %[f,revertclass] = tofloat(f); PQ = paddedsize(size(f)); [U,V] = dftuv(PQ(1),PQ(2)); D = hypot(U,V); D0 = 0.05*PQ(2); F = fft2(f,PQ(1),PQ(2)); H = exp(-(D.^2)/(2*(D0^2))); g = dftfilt(f,H); g = im2uint8(g); %g = revertclass(g); subplot(222);imshow(fftshift(H)); title(‘高斯低通滤波器图像‘); %显示滤波器图像 subplot(223);imshow(log(1+abs(fftshift(F))),[]);title(‘滤波器的谱‘); subplot(224);imshow(g);title(‘滤波器后的图像‘)
各种滤波器的传递函数不同,但是滤波的过程是一样的,因此,可以将这几种滤波器封装成一个函数,如下:
%频率域低通滤波函数,生成几个低通滤波器的传递函数
function [H,D] = lpfilter(type,M,N,D0,n)
[U,V] = dftuv(M,N);
D = sqrt(U.^2+V.^2);
switch type
case ‘ideal‘
H=double(D<=D0);
case ‘btw‘
if nargin ==4
n=1;
end
H=1./(1+(D./D0).^(2*n));
case ‘gaussian‘
H=exp(-(D.^2)./(2*(D0^2)));
otherwise
error(‘unkown filter type‘);
end
原文:https://www.cnblogs.com/libai123456/p/11441075.html