
本文的出发点是一篇期刊论文,但集中探讨的是这篇文章中不确定度估计的原理与过程,行文将与之前的文献报告不同。
原文
Bhattacharyya A , Fritz M , Schiele B . Long-Term On-Board Prediction of People in Traffic Scenes under Uncertainty[J]. 2017.
原文的一篇重要引用文献
Kendall A , Gal Y . What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision?[J]. 2017.
关键词与基础概念:
车载视角、行人框预测、认知不确定性、偶然不确定性、采样、伯努利分布与dropout变分推断、蒙特卡洛积分、贝叶斯定理与贝叶斯推断、贝叶斯网络
近日在阅读“Long-Term On-Board Prediction of People in Traffic Scenes Under Uncertainty”,文章所提出的模型功能是基于车载移动视角对行人框位置做出预测,并能够同时评估两类不确定度(模型不确定度,数据不确定度)。
对神经网络的不确定度估计涉及较多概率论的知识,而且从理论到应用的转化也涉及到使用近似量估计的问题,因此初次接触这部分知识该我带来了不小的挑战。经过几天的探究,还是走了不少弯路,虽说很多细节的理论推理还没有深究,但摸清了借助贝叶斯神经网络估计不确定度的原理和过程。你会发现,在原有神经网络上增加不确定度估计功能,从结构上的变化看似非常简单(只是损失函数,dropout层,输出等已有部分的修改),但背后有很严密的数理逻辑驱动着。
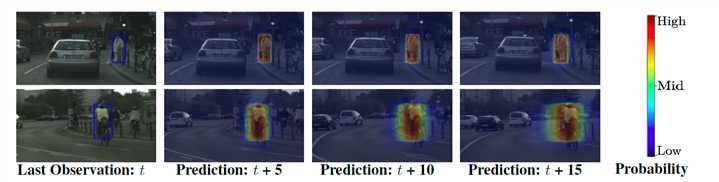
不确定度虽分为两类,一类是模型不确定性,另一类是数据不确定性,两种不确定性所在的对象不同。利用模型预测结果的分布特点(注意是分布),可以成为测量不确定度的一种手段。
模型预测由模型生成,在给定训练数据情况下,模型自身有后验分布(因此用不确定度衡量)。为了得到模型预测的分布特点,由贝叶斯定理,需要边缘化(marginalizing,旨在消除条件分布中某个变量的影响)模型的后验分布。
从理想层面,边缘化就是以积分形式穷尽所有模型的分布最后得到模型预测的分布,但现实层面由于深度网络的复杂性,有两方面不现实 - 模型表示的抽象性 & 积分操作,为了落地,在应用时,理想的“积分操作”由离散的采样操作代替(因为我们最终不需要预测分布的完整描述,只需方差即可,而基于dropout的采样方式被证明可以求出方差)。
理想的模型分布是无法满足采样需求的,因此需引入近似模型分布的可采样的分布,新引入的分布由诸多参数决定着,要想近似原模型分布必须要进行参数调整,一种方法是最小化近似分布和原分布的KL散度指标,而这恰好是一个带有明确目标函数的优化任务。至此,对预测分布求解实现了从理论的边缘化操作到实际的优化操作(可通过反向传播)+采样的转换。
该部分简单介绍期刊文章的模型框架,旨在为后文不确定性公式推理建立规范和基础。
车载视角的行人轨迹预测需要考虑两个重要方面,一是行人的轨迹,二是车辆的里程计(速度和转向角)。为此模型专门设计了两条序列流负责这两个方面特征:
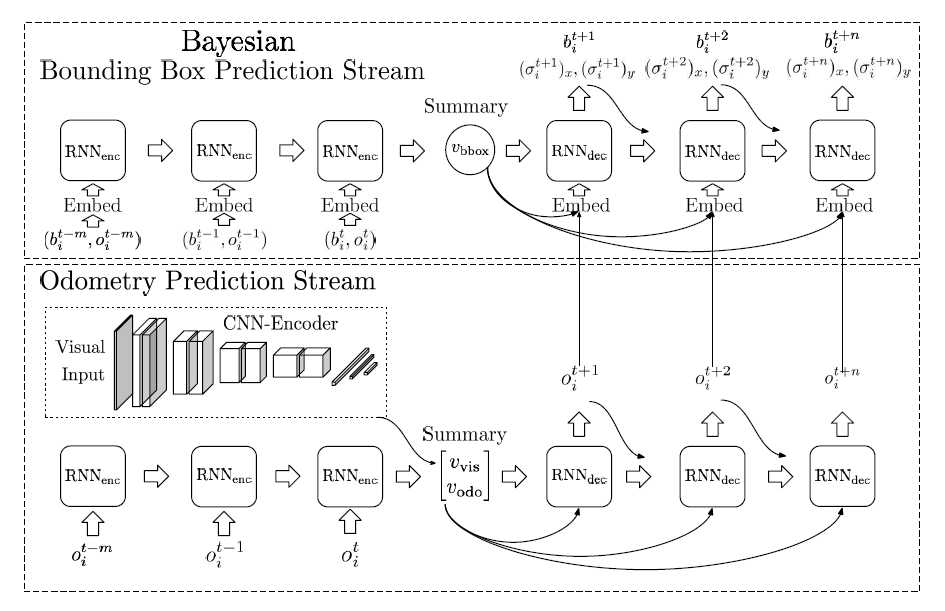
里程计:\(o^t = (s^t,d^t)\)表示速度和转向角,\(O_p=[o^{t-m},...,o^{t}]\)表示已知里程计信息,\(O_f=[o^{t+1},...,o^{t+n}]\)表示里程计流预测的里程计。
行人框:\(b_i^t = \{(x_{tl},y_{tl}),(x_{br},y_{br})\}\),\(B_p = [b_i^{t-m},...,b_i^{t}]\)表示已知行人框信息,\(B_f=[b_i^{t+1},...,b_i^{t+n}]\)表示预测的行人框。除此之外,还有\(\sigma_x,\sigma_y\),这些是在假设模型观测噪音为高斯分布后所设立的(后文会介绍)
预测分布:最终所求不确定性所依赖的预测分布具体指的就是\(B_f\)的后验分布。
\(B_f\)是行人框预测流输入\(B_p,O_p,O_f\)所产生的,因此\(B_f\)的后验分布可以写成:
\[p(B_f|B_p,O_p,O_f)\]
当然,若考虑由数据库真值\(\{X,Y\}\)推断出模型的概率分布\(p(f|X,Y)\)(f是模型),\(B_f\)的后验分布更准确地写成:
\[p(B_f|B_p,O_p,O_f,X,Y)\]
在贝叶斯模型中,有两类主要的不确定性:模型不确定性和数据不确定性。
下图是一个逐像素级别的不确定度估计,应用场景是CV常见的semantic segmentation。
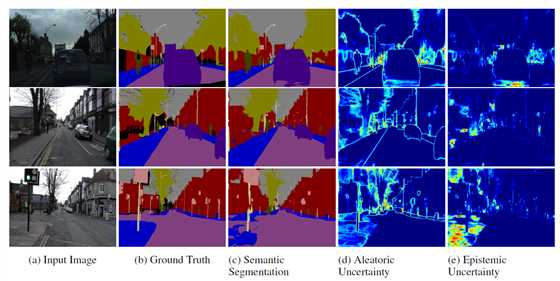
根据之前不确定性的分类介绍,我们也可以大致感受到需要重点考虑的模型不确定性,因此文章中也花大篇幅来讲这个方面。
Part1 - 用简化分布拟合真实模型分布
模型不确定性可通过模型的预测分布来求得,具体来说就是预测分布的方差。要得到预测结果的后验分布,由贝叶斯定理,我们可以这样求出:
\[p(B_f|B_p,O_p,O_f,X,Y) = \int p(B_f|B_p,O_f,O_p,f)p(f|X,Y)df\]
这其实就是考虑模型\(f\)的所有情况,而后将\(f\)的每种情况经\(\{X,Y\}\)推理出的后效概率乘以在该情况下预测的分布,将所有情况累加起来就是预测分布。
但是,理论很丰满,现实很骨感,看看这个式子就知道实际操作是不现实的,主要有\(f\)代表的模型表述抽象和积分操作难达成两个方面的问题。因此,在实际操作时模型做了简化:
简化一 - 将抽象的模型\(f\)用模型中有限的参数\(w\)表示:
\[p(B_f|B_p,O_p,O_f,X,Y)=\int p(B_f|B_p,O_f,O_p,w)p(w|X,Y)dw\]
简化二(基于简化一) - 将不可求的\(p(w|X,Y)\)分布用简化的伯努利分布\(q(w)\)代替,使得dropout采样操作能够顺利进行(采样稍后要用到,本质是用离散的数据点去近似求积分):
\[p(B_f|B_p,O_p,O_f)=\int p(B_f|B_p,O_p,O_f,w)q(w)dw\]
*由于\(\{X,Y\}\)实际上是笼统指代,在实际问题中\(X={B_p,O_p,O_f},Y={B_f}\),因此最后写成的条件概率表达式也省略了这个部分。
Question - 为什么采用伯努利分布?
如果再仔细观察一下\(q(W_k)=M_k \centerdot diag([z_{i,j}]^{C_k}_{j=1})\)这个定义的简单分布,若将\(M_k\)等价于模型中原有的权重矩阵,那么这个分布在采样(sample,在连续的分布上采样,从而产生样本点)实际上和机器学习中流行的dropout层概念是一致的,将某列指令表示将该神经元失活。
事实上,当把这个分布落实到本文中RNN的Encoder和Decoder上时,这是这样操作的。
Part2 - 仅需预测分布的方差?用采样替代积分吧!
Part1中的预测分布经多次简化后最后得到式子如下:
\[p(B_f|B_p,O_p,O_f)=\int p(B_f|B_p,O_p,O_f,w)q(w)dw\]
可以看到,公式中还是存在积分运算,要实际使用还是有困难。不过,我们获取预测分布的目的是用分布方差代表模型不确定,要估计方差不需要大费周章地用积分把整个分布求出来,仅需采样一定规模的样本点就可以估计。
\(p(B_f|B_p,O_p,O_f)\)的具体采样过程:在伯努利分布的\(q(w)\)采样得到\(w\)的样本\(w^t\),再用\(w^t\)所代表的模型生成预测\(b^t\),\(b^t\)即为预测分布的一个采样样本点。因此对预测分布的采样是通过对\(q(w)\)采样间接实现的。(合理性在总结部分有说明原因)
假设采样了T次,最终预测分布的方差:
\[Var(epistemic)={1 \over T}({\Sigma^T_{i=1}(\hat b_i^t)^T \hat b_i^t - {1 \over T}(\Sigma^T_{i=1}(\hat b_i^t)^T)(\Sigma^T_{i=1}\hat b_i^t))}\]
用方差代表不确定度对模型进行评估已经属于训练后的测试阶段,是\(q(w)\)中参数已经优化好后的行为(因为这样才能代表原始的\(p(f|X,Y)\))。
而在伯努利分布上采样其实就是dropout操作,但此时dropout是在测试阶段使用的,并且目的与传统的防止过拟合也不同了。
Part3 - 简化分布中参数的优化
Part1中定义的伯努利变换\(q(w)\)是具有参数的,参数恰当,\(q( w)\)才能是\(p(w|X,Y)\)的恰当估计。因此我们还需要根据评价指标对其中的可变参数\(M_k\)进行优化,KL散度是评价真实分布和拟合分布相关性的指标,当完全拟合时为零。
文章中对KL散度进行了演算,最后得到的右边部分(演算过程我没有深究):
\[KL(q(w)||p(w|X,Y))\ \propto KL(q(w)||p(w)) - \Sigma_t\int q(w)log(b_t^{t+n}|b_t^{t+n-1},B_p,O_p,O_f,w)dw\]
*\(\propto\)代表成比例,演算将原KL散度转换成了两部分:\(q(w)\)与先验分布的散度、与数据有关的负似然部分。
如果我们将KL散度推导式作为目标函数进行神经网络训练,那么在右边部分我们还是可以看到有对\(w\)的积分,在实现时,我们使用蒙特卡洛积分替代原有积分,其本质也就是以一定策略根据多次对\(w\)采样估计出积分的大小。同时我们假设模型预测噪音呈现4-D的高斯分布,\(N(b_i^t,\Sigma_i^t)\)(其中\(\Sigma_i^t\)是\(diag(\sigma_x^t,\sigma_y^t,\sigma_x^t,\sigma_y^t)\)的对角矩阵)。
KL推导式负似然对数部分:通过解析模型输出得到高斯分布的参数\((b_i^t,\Sigma_i^t)\),使用PDF算法就可以求出(log和PDF公式中的e指数抵消了)。
KL推导式函数的KL散度部分:当权重参数的先验分布是均值为0的高斯分布时,KL散度恰好对应就是L2正则化。
相比KL推导式,目标函数新增的:\(log(\hat \sigma_i^2)\)这部分是新提出的,为了防止模型把方差\(\Sigma_i\)弄得巨大以至于负似然对数部分的损失变为0了。
针对本文的实际场景,最终模型的优化目标就是:
\[Loss = {1 \over 4N}\Sigma^N_i \Sigma^n_j||\hat b_i^{t+j}-b_i^{t+j}||^2_2(\hat \Sigma _i^{t+j})^{-2}+\lambda \Sigma_W||W_k||_2+log(\hat \sigma_i^2)\]
参数优化属于训练部分,而估计积分大小时对\(w\)进行了采样,采样操作其实又dropout操作,但此时dropout的目的不在于防止过拟合,而是采样。
Question - Dropout 辨析
至此,本文模型中对于dropout操作的辨析有两个方面:
- 测试阶段和训练阶段dropout均要使用,目的是对模型参数的伯努利分布进行采样,但是训练是为了蒙特卡洛积分以估计连续积分,而测试是估计模型不确定性。
- 本文两处使用dropout的目的与传统避免过拟合的目的是不同的。
相比模型,数据不确定性的估计在神经网络中见得更多(例如Social LSTM的二维高斯分布假设),本文也沿用这样的方式,假设RNN解码器输出的数据满足4-D高斯分布,通过解析这些数据得到高斯分布的参数\(N(b_i^t,\Sigma_i^t)\)(和上文所假设的一致),那么数据不确定性就可被视作:
\[Var(Aleatoric)={1 \over T}((\Sigma^T_{i=1}(\hat \sigma_i^t)_x+\Sigma_{i=1}^T(\hat \sigma_i^t)_y)\]
*T是在估测模型不确定性时的采样次数
与模型不确定性的评估方式不同,我们是直接让模型输出数据不确定性,而不是分析同一组输入经多个模型样本得到的输出的统计性质。
Question - 方差预测并没有对应的label进行监督,在训练时又是如何引导模型正确估计方差的呢?
请看上文中的Loss函数定义,与输出方差有关的有:\((\hat \Sigma_i^{i+j})^{-2}\)和\(log(\hat \sigma_i^2)\)。现在不妨将其方差的意义抹去,只看做输出的一个参数:
- 首先,上述该参数有关的两部分互相牵制,限制参数在一个合理区间上(不会过大或过小)。
- 其次,\((\hat \Sigma_i^{i+j})^{-2}\)要实现的功能是令Loss函数加重对某些性质数据的关注,同时减小对某些性质数据的关注,从认知角度上来说,置信度高(噪音低)的更应该被关注,因为这样使得Loss函数对噪音更优抵抗力,因此该参数被训练成表示噪音高低,这恰好与方差的意义对应上了。
*上述这些在论文中都是在实验完成后基于概率论理论进行的后验解释。
\[Var = Var(epistemic) + Var(Aleatoric)\]
由不确定性的计算:通过输入含有观测噪音的数据,透过在模型分布上多次采样得到的模型样本,得到输出的样本,这些样本所在的分布主要由数据和模型分布所决定的,通过分析样本分布的特点,就综合得到了数据和模型的分布特点,进而得到两类不确定性。
阅读了部分参考文献,看了许多与贝叶斯网络和概率论相关的博客,感觉对文章中一些理论理解还是比较模糊,主要还是由于这个方面的基础知识比较欠缺,许多概念和约定意义都不了解。不过,现阶段对“不确定性”估计还是有些体会(也许是错误的),写在这里:
不确定性-犯罪者?受害者?伤害评定?:
贝叶斯神经网络:传统意义上的神经网络中,我们研究的是权重的值,并根据训练数据\(\{X,Y\}\)进行优化;而在贝叶斯神经网络中,我们研究的是权重的分布,一个贝叶斯网络可以被等价视为无限个同结构的传统神经网络,并且伴随着由\(\{X,Y\}\)所决定的概率分布。
本文行人框流模型的实质:一个带有dropout层的贝叶斯神经网络框架,实现从输入数据到行人框、方差(偶然不确定性)的映射功能,并完成认知不确定性的近似。
神经网络的两类优化目标:根据是否了解神经网络参数有的先验概率,我们将神经网络优化策略分为Maximize Likelihood Estimation(最大化似然估计)和Maximize Aposteriori Estimation(最大化后验概率估计)。可以形象地理解为,在优化参数时,MLS将力求做到对于训练数据中的\(\{X,Y\}\),输入X模型将力求输出为Y的概率为最大,而MAP除了考虑数据以外,其还要考虑参数的先验分布;MLS纯粹地数据依赖性使得在你不清楚模型在做什么的情况下都能做出预测结果,但是弊端很明显在于数据的质量,例如小样本的投硬币实验很可能使得模型对投硬币概率做出错误的估计。
\(KL(q(w)||p(w|X,Y))\)通用化简过程:
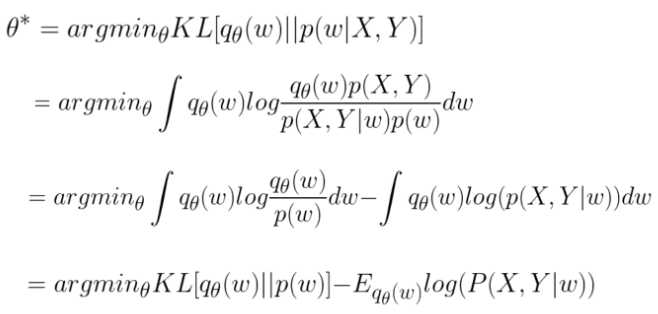
友情链接:重要的学习资料。同时,在学习过程中走了不少弯路,但觉得有些弯路还是值得记下来以备后续使用的。
说在最后,本文是笔者第一次接触贝叶斯网络与相关的概率论知识,纵使查阅诸多资料,但短时间内对该部分内容掌握通透还是不现实,文中也可能存在一些错误和理解偏差,敬请读者阅读时多加留意和思考,也欢迎指出文章中的问题。
笔记 - 基于贝叶斯网络的不确定估计(从一篇车载视角的行人框预测论文出发)
原文:https://www.cnblogs.com/sinoyou/p/11441634.html