支持向量机

硬间隔：

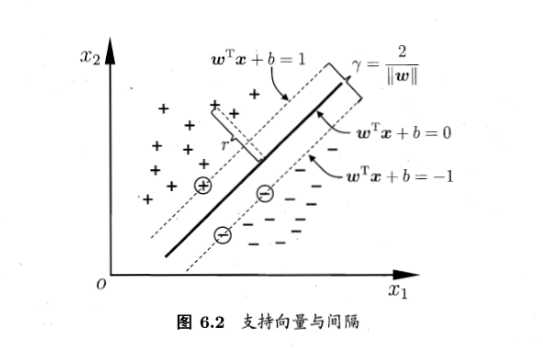
超平面通过如下方程描述：

　　$w^{T}x+b=0$

则任意一点到超平面的距离：

　　$r=\frac {|w^{T}x+b|} {||w||}$

假设超平面(w,b)能将训练样本正确分类，即对于$(x_{i},y_{i})\subset D$，若$y_{i}=+1$，则有$w^{T}x_{i}+b>0$，若$y_{i}=-1$，则有$w^{T}x_{i}+b<0$。令

　　$\left\{\begin{matrix}w^{T}x_{i}+b \geq 1,y_{i}=+1\\ w^{T}x_{i}+b \leq  1,y_{i}=-1\end{matrix}\right.$

因为$w^{T}x+b$前面可以乘以一个常数而超平面不变，所有令$w^{T}x+b=1$，则最大化

　　$\gamma = \frac {2}{||w||}$

即：

　　$\underset{w,b}{max} \frac {2}{||w||}$

　　$s.t. \ y_{i}(w^{T}x_{i}+b)\geq 1,i=1,2,...,m$

等价于：

　　$\underset{w,b}{min} \frac {1}{2}||w||^{2}$

　　$s.t. \ y_{i}(w^{T}x_{i}+b)\geq 1,i=1,2,...,m$

对偶问题：

　　$L(w,b,a)=\frac{1}{2}||w||^{2}+\sum_{i=1}^{m}a_{i}(1-y_{i}(w^{T}x_{i}+b))$

对w和b求导：

　　$w=\sum_{i=1}^{m}a_{i}y_{i}x_{i}$

　　$0=\sum_{i=1}^{m}a_{i}y_{i}$

支持向量机

原文：https://www.cnblogs.com/xcxy-boke/p/11455981.html