https://cn.vjudge.net/problem/UVA-12165
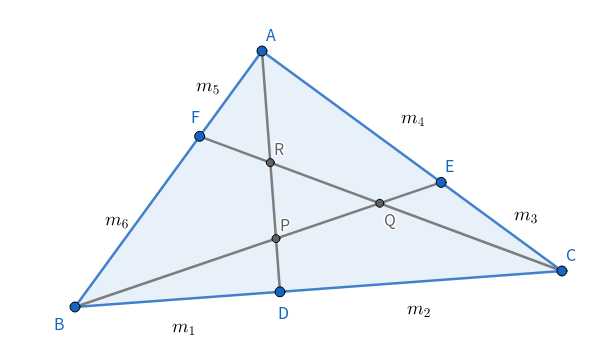
给出D、E、F分BC,CA,AB的比$m_1:m_2$,$m_3:m_4$,$m_5:m_6$和PQR三点的坐标,求ABC三点的坐标
利用梅涅劳斯定理,找出直线和三边的交点,然后每个边按顺序乘下去
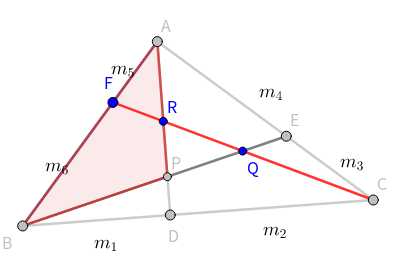
可以写出三个方程
\[\frac{AR}{RP}\cdot\boxed{\frac{PQ}{QB}}\cdot\frac{BF}{FA}=1\]
\[\frac{BP}{PQ}\cdot\boxed{\frac{QR}{RC}}\cdot\frac{CD}{DB}=1\]
\[\frac{CQ}{QR}\cdot\boxed{\frac{RP}{PA}}\cdot\frac{AE}{EC}=1\]
然后得到
\[\frac{AR}{RP}\cdot\frac{PQ}{PQ+BP}=\frac{m5}{m6}=k_1\]
\[\frac{BP}{PQ}\cdot\frac{QR}{QR+RC}=\frac{m1}{m2}=k_2\]
\[\frac{CQ}{QR}\cdot\frac{RP}{RP+RA}=\frac{m3}{m4}=k_3\]
最后解
\[x_1=k_1(1+x_2)\]
\[x_2=k_2(1+x_3)\]
\[x_3=k_3(1+x_4)\]
然后点加向量就可以得出三点坐标
AC代码
#include<cstdio>
#include<cctype>
#include<cmath>
#define REP(r,x,y) for(register int r=(x); r<(y);r++)
#ifdef sahdsg
#define DBG(...) printf(__VA_ARGS__)
#else
#define DBG(...) (void)0
#endif
using namespace std;
int _s; char _c;
template <class T>
inline void read(T&x) {
x=0;
do _c=getchar(); while(!isdigit(_c) && _c!=‘-‘);
_s=1;
if(_c==‘-‘) _s=-1, _c=getchar();
while(isdigit(_c)) { x=x*10+_c-‘0‘; _c=getchar();} x*=_s;
}
template<class T, class...A> inline void read(T &x, A&...a){read(x); read(a...);}
#define D point
#define CD const D
struct point {
double x,y;
void read() {scanf("%lf%lf",&x,&y);}
void prn() {printf("%.8lf %.8lf",x,y);}
};
D operator+(CD&l, CD&r) {return (D){l.x+r.x,l.y+r.y};}
D operator-(CD&l, CD&r) {return (D){l.x-r.x,l.y-r.y};}
D operator/(CD&l,double a) {return (D){l.x/a,l.y/a};}
D operator*(CD&l,double a) {return (D){l.x*a,l.y*a};}
D operator*(double a, CD &l) {return (D){l.x*a,l.y*a};}
double cross(CD&l, CD&r) {return l.x*r.y-l.y*r.x;}
D intersec(CD&a, D b, CD&c, D d) {
b=b-a; d=d-c; D u=a-c;
double t = cross(d, u) / cross(b,d);
return a+b*t;
}
#undef CD
#undef D
point P,Q,R,A,B,C;
#define x1 nvdsaokvl
#define x2 nvkjdavnf
#define x3 vmasdvddz
int m1,m2,m3,m4,m5,m6;
double k1,k2,k3,x1,x2,x3;
int main() {
int N; read(N);
while(0<N--) {
P.read(); Q.read(); R.read();
read(m1,m2,m3,m4,m5,m6);
k1=(double)m5/m6, k2=(double)m1/m2, k3=(double)m3/m4;
double t=1-k1*k2*k3;
x1=(k1+k1*k2*k3+k1*k2)/t;
x2=(k2+k1*k2*k3+k2*k3)/t;
x3=(k3+k1*k2*k3+k1*k3)/t;
DBG("%lf %lf %lf\n", x1,x2,x3);
A=x1*(R-P)+R;
B=x2*(P-Q)+P;
C=x3*(Q-R)+Q;
A.prn();putchar(‘ ‘);
B.prn();putchar(‘ ‘);
C.prn();putchar(‘\n‘);
}
return 0;
}
原文:https://www.cnblogs.com/sahdsg/p/11470498.html