目录
一、概述
栈跟队列都是保存数据的容器。还有前面的线性表。
栈和队列主要用于计算过程中保存的临时数据,如果数据在编程时就可以确定,那么使用几个变量就可以临时存储,但是如果存储的数据项数不能确定,就需要复杂的存储机制。这样的存储机制称为缓存。栈和队列就是使用最多的缓存结构。
1、栈、队列和数据使用顺序
栈和队列是最简单的缓存结构,它们只支持数据项的存储和访问,不支持数据项之间的任何关系。因此,它们最重要的两个操作就是存入元素和取出元素。
当然还有其他的操作,比如创建,检查空(或者满)的操作。
按照数据在时间上生成的先后顺序进行不同的处理:
那么如何实现这两种结构呢,最自然跟最简单的实现方式就是使用线性表。
2、应用环境
很多,从略。python中可以直接使用list实现栈的功能。可以使用deque,实现队列的功能。
二、栈:概念和实现
存入栈中的元素之间没有任何具体关系,只有到来的时间先后顺序。因此,就没有元素的位置和元素的前后顺序等概念。
栈的基本性质保证,在任何时刻可以访问、删除的元素都是在此之前最后存入的那个元素。
1、栈抽象数据对象

栈的线性表实现相关问题
在线性表的一端进行插入和删除操作,这一端称为栈顶,另一端称为栈底。
对于顺序表,后端插入和删除是O(1)操作,因此考虑使用这一端作为栈顶。
对于链接表,前端插入和删除是O(1)操作,因此用这端作为栈顶。
2、栈的顺序实现
把list直接当做栈使用,也是可以的,只是这样的对象跟list无法区分,并且提供了栈不应该支持的list所有操作,这样就会威胁到栈的安全。

class StackUnderFlow(ValueError): ‘‘‘ 栈下溢,也就是空栈访问 ‘‘‘ pass class SStack: def __init__(self): self.elems = [] def is_empty(self): return self.elems == [] def push(self, elem): self.elems.append(elem) def pop(self): if self.is_empty(): rasise StackUnderFlow(‘in SStack pop‘) return self.elems.pop() def top(self): if self.is_empty(): raise StackUnderFlow(‘in SStack top‘) return self.elems[-1]
3、栈的链接表实现
顺序表实现的优缺点:
采用链接表实现的优点,不需要一个连续的存储块就可以,而且没有替换存储的高代价操作。但是它的缺点零散的存储比较依赖python的存储管理,还有每个结点的链接也会带来开销。

class LStack: def __init__(self): self.top = None def is_empty(self): return self.top is None def push(self, elem): self.top = LNode(elem, slef.top) def pop(self): if self.is_empty(): raise StackUnderFlow(‘in LStack pop‘) e = self.top.elem self.top = self.top.next return e def top(self): if self.is_empty(): raise StackUnderFlow(‘in LStack top‘) return self.top.elem
三、栈的应用
栈的用途主要是两方面:

s1 = SStack() for i in list1: s1.push(i) list2 = [] while not s1.is_empty(): list2.append(s1.pop())
1、简单应用:括号匹配问题
问题:
分析:
实现过程:

def check_parens(text): ‘‘‘ 括号配对检查函数,text是被检查的正文串 ‘‘‘ one_parens = ‘[{(‘ opposite = {‘]‘:‘[‘,‘)‘:‘(‘,‘}‘:‘{‘} st = SStack() for s in text: if s in one_parens: st.push(s) if s in opposite and st.pop() != opposite[s]: return False if st.is_empty(): #书中没有最后这一步的判断。 return True else: return False
2、表达式的表示,计算和变换
表达式和计算的描述
我们常用的表达式是用二元运算符连接起来的中缀表达式。例如:(1+2)*3
中缀表达式是习惯的表达式,但是它有一些缺点,比如不能准确描述计算的顺序,通常需要借助一些辅助符号(比如圆括号),或者优先级(比如先乘除后加减)。
比如上面的例子中,如果没有(),那么计算顺序将会完全不一样。
因此,当计算机处理表达式的时候,通过会把中缀表达式转化为后缀表达式(逆波兰表达式)。当然,还有一种表达式是前缀表达式(波兰表达式)。
后缀表达式和前缀表达式都不需要括号或者优先级,或者结合性的规定。
例子:
中缀形式:(3-5) * (6+17*4) / 3
前缀形式:/ * - 3 5 + 6 * 17 4 3
后缀形式:3 5 - 6 17 4 * + * 3 /
后缀表达式的计算
分析后缀表达式的计算规则
遇到问题:
解决方法:
为判断不足两个元素的情况,必须给栈添加一个属性(写成方法也可以),就是栈的深度。

def suffix_exp_evaluator(line): ‘‘‘ 将表达式的字符串变为项的表 ‘‘‘ return suf_exp_evaluator(line.split()) class ESStack(SStack): @property def depth(self): return len(self.elems) class suf_exp_evaluator(exp): oper = ‘-+*/‘ st = ESStack() for x in exp: if x not in oper: st.push(float(x)) continue a = st.pop() b = st.pop() if x == ‘+‘: c = a + b elif x == ‘-‘: c = b - a elif x == ‘*‘: c = a * b elif x == ‘/‘: c = b / a else: break st.push(c) if st.depth == 1: return st.pop() raise SyntaxError(‘Extra operand(s)‘)
中缀表达式到后缀表达式的转换
在中缀表达式转换后缀表达式中要注意两点:

infix_operators = ‘+-*/()‘ def tokens(lines): ‘‘‘ 生成器函数,逐一生成line中的一个个项。项是浮点数或者运算符。 本函数不能处理一元运算符,也不能处理带符号的浮点数。 ‘‘‘ i, llen = 0, len(line) while i < llen: while i < llen and line[i].isspace(): i += 1 if i >= llen: break if line[i] in infix_operators: yield line[i] i += 1 continue j = i + 1 while (j < llen and not line[j].isspace() and line[j] not in infix_operators): if ((line[j] == ‘e‘ or line[j] == ‘E‘) and j+1 < llen and line[j+1] == ‘-‘): # 处理负指数 j += 1 j += 1 yield line[i:j] i = j def trans_infix_suffix(line): st = SStack() exp = [] for x in tokens(line): # tokens是一个待定义的生成器 if x not in infix_operators: # 运算对象直接送出 exp.append(x) elif st.is_empty() or x == ‘(‘: # 左括号进栈 st.push(x) elif x == ‘)‘: # 处理右括号的分支 while not st.is_empty() and st.top() != ‘(‘: exp.append(st.pop()) if st.is_empty(): # 没找到左括号,就是不配对 raise SyntaxError("Missing ‘(‘.") st.pop() # 弹出左括号,右括号也不进栈 else: # 处理算术运算符,运算符都看作是左结合 while (not st.is_empty() and priority[st.top()] >= priority[x]): exp.append(st.pop()) st.push(x) # 算术运算符进栈 while not st.is_empty(): # 送出栈里剩下的运算符 if st.top() == ‘(‘: # 如果还有左括号,就是不配对 raise SyntaxError("Extra ‘(‘.") exp.append(st.pop()) return exp
3、栈与递归
递归满足两个条件:
递归调用的过程
以阶乘函数为例:
def fact(n): if n == 0: return 1 retrun n * fact(n-1)
看一下fact(3)的计算过程:
我们把这种栈称为程序运行栈。
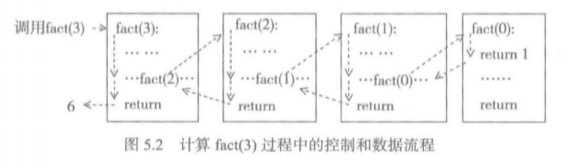
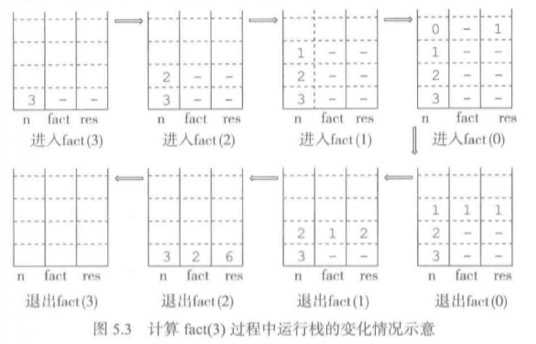
上面两幅图分别描述了fact(3)的调用和返回过程和它的程序运行栈信息变化。
栈和递归/函数调用
一般而言,对于递归函数,其执行的时候都有局部状态,包括函数的形参和局部变量等数据,递归函数在调用自己之前需要先把这些变量保存在程序运行栈中,以备后来使用。
编程语言实现递归函数就是运行一个栈,每个递归函数调用都在栈上开辟一块区域,称为函数帧,用来保存相关信息。位于栈顶的帧是当前帧,所有局部变量都在这里。在进入下一个递归调用时,再建立一个新帧。当函数从下一层递归中返回时,递归函数的上一层执行取得下层函数调用的结果,执行弹出已经结束的对于的帧,然后回到调用前的那一层的执行状态。
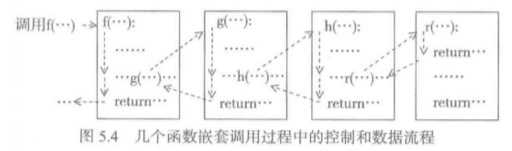
其实不只是递归函数,实际上一般函数的调用和退出的方式也与此类似。例如上图中,在f里调用g,在g中调用h,在h中调用r。也是使用程序运行栈来保存局部数据。
当然,一般函数的调用跟递归函数调用还是有不同的,比如一般函数调用的每个函数局部状态不同,因此,他们的参数个数,局部变量的个数就不同,那么在分配函数帧的容量时就不同。
栈与函数调用*
在程序执行中,函数的嵌套调用是按照‘后调用先返回’的规则进行的,这种规则符合栈的使用模式,因此栈可以很自然的支持函数调用的实现。
函数调用时的内部动作分两部分:
函数的前序动作包括:
函数的后序动作包括:
每次函数的调用都要执行这些动作,因此可以看出函数调用是有代价的。
递归与非递归
对于递归函数的调用,实际上就是把信息保存到运行栈中,然后不断执行函数体的那段代码。因此,完全可以修改递归函数,将其变成一个非递归函数。

def norec_fact(n): ‘‘‘ 自己管理栈来模拟函数调用的过程。 ‘‘‘ res = 1 st = SStack() while n > 0: st.push(n) n -= 1 while not st.is_empty(): res *= st.pop() return res
递归函数和非递归函数
任何一个递归函数都可以通过引入一个栈来保存中间结果的方式,翻译为一个非递归函数。同理,任何一个包含循环的程序也可翻译成一个不包含循环的递归函数。
在目前的新型计算机上,函数调用的效率多半都可以接受,通常如果递归的思想比较简单,不一定要用非递归函数定义。当然,除了一些对效率要求特别高的特殊情况之外。
栈的应用:简单背包问题
问题:一个背包可以放重量为w的物品,现在有n件物品,它的集合是S,重量分别是w0,w1,...wn-1。然后,从中挑选出若干件物品,它们的重量之和正好等于w。如果存在,就说这个背包问题有解,如果不存在就无解。
先考虑递归思想的求解思路。
现在用knap(w, n)表示n件物品相对于总总量w的背包问题,那么在通常考虑一件物品选还是不选,有两种情况:
那么n件物品的背包问题就变成了n-1件物品的背包问题。区别就是,一种情况是重量一样,种类减一。一种情况是重量少了,种类减一。

def knap_rec(weight, wlist, n): if weight == 0: return True if weight < 0 or (weight > 0 n < 1): return False if knap_rec(weight-wlist[n-1], wlist, n-1): return True if knap_rec(weight, wlist, n-1): return True else: return False
四、队列
1、队列抽象数据类型

2、队列的链接表实现
没有尾指针的实现,如果把链表尾端作为队头,那么加入队列的时间复杂度复杂度是O(n),而从队列中取出元素的操作(也就是从链表首端删除第一个元素)时间复杂度是O(1)。
如果有尾指针,上面的两个操作都是O(1)的时间复杂度。
具体实现很简单,跟前面的链表类似。
3、队列顺序表实现
基于顺序表实现的问题
利用顺序表现有的结构实现队列:
这两种情况都有一个O(n)操作,因此都不理想。
还有一种是在队首出队之后,元素不前移,只需要记住新队头的位置就可以。这个设计虽然能达到O(1)的操作,但是有一个致命的问题,随着不断的入队元素,队列前面会有越来越多的空位,并且这些空位永远不会被利用,这就浪费了存储资源。详情见下图。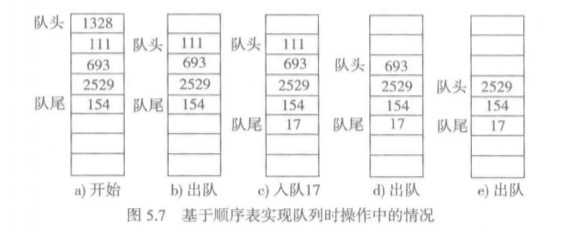
因此,以上的设计都不是最合理的。
循环顺序表
如果把顺序表看做一个环形结构,认为其最后存储位置之后是最前的位置,形成一个环形。那么就会循环利用空间,解决了队首出现空位的情况。
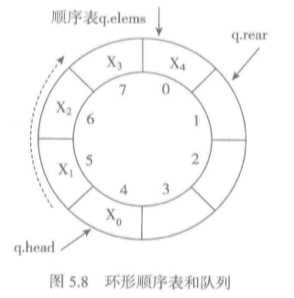
上图是一个包含8个元素的顺序表
注意变动操作维护上面变量的值,出队和入队时变量更新操作。
q.head = (q.head+1)%q.len
q.rear = (q.rear)%q.len
队空操作。q.head == q.rear
队满操作。(q.rear+1)%q.len = q.head
此外,当队满的时候进行存储空间扩充。这里很难利用list的自动扩充机制,因此需要自己管理list的存储。
4、队列list实现
数据不变式
队列里设计到四个属性,head,rear,num,len。还有一些变动属性的操作。因此,在进行变动操作的时候就应该遵守数据不变式的原则,维护数据的正确性。
数据不变式说明对象的不同属性,描述它们应该满足的逻辑约束关系,如果一个对象的成分取值满足数据不变式,就说明这是一个状态完好的对象。
队列类的实现

class SQueue: def __init__(self, init_len=8): self.head = 0 self.num = 0 self.len = init_len self.elems = [0] * self.len def is_empty(self): return self.num == 0 def peek(self): if self.is_empty(): raise ValueError return self.elems[(self.head] def dequeue(self): if self.is_empty(): raise ValueError e = self.elems[self.head] self.head = (self.head + 1) % self.len self.num -= 1 return e def enqueue(self, elem): # 表满的时候,需要扩充。 if self.num == self.len: self.extend() self.elems[(self.head + self.num)%self.len] = elem self.num += 1 def extend(self): ‘‘‘ 表的扩充采用2倍的策略。并且是新表的头是从下边0开始。 也可以采用新表的头跟原表的下标一样的策略。看设计需求。 ‘‘‘ old_len = self.len self.len *= 2 new_elems = [0] * self.len for i in range(old_len): new_elems[i] = self.elems[(self.head+i)%old_len] self.elems, self.head = new_elems, 0
5、队列的应用
五、迷宫求解和状态空间搜索
1、迷宫求解:分析和设计
迷宫问题
问题:给定一个迷宫图,包括图中的一个入口点和出口点。要求找到一条从入口到出口的路径。
初步分析:
迷宫问题分析
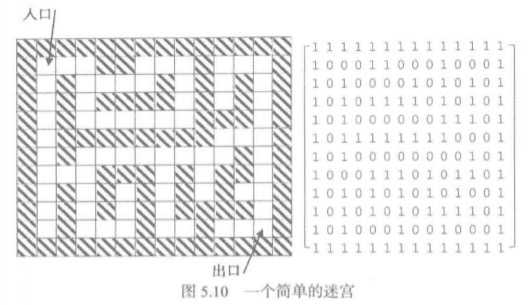
分析问题
这个过程显然需要缓存一些信息:如果当前位置有多个方向可供探查,但是下一步只能探查一个方向,因此需要记录其他暂时不能探查的方向,以后后面使用。
那么该使用什么方式进行缓存呢?
存在两种不同的方式,可以比较冒进,也可以稳扎稳打。
问题表示和辅助结构
迷宫本身使用一个元素值为0/1的矩阵表示,在python中可以用嵌套list表示。迷宫的入口和出口各用一个下标表示。
有一个特殊情况,在探索过程中可能会出现兜圈子的情况,为防止这种情况,必须采用某种方法记录已经探查过的位置信息。
这种位置信息有两种方式表示:
现在假设使用一个矩阵表示迷宫图,0表示通路,1表示非通路,2表示已经探查过的路径。
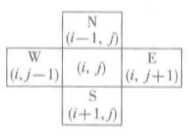
表示当前位置的可行方向。假设用一个二元组表示元素位置(i,j)。i和j分别元素是在矩阵中的下标。那么它的四个方向通过上图就可以表示出来。
此外,还应确定一个位置可探查方向的顺序,在这里规定为‘东南西北’。
2、求解迷宫的算法
迷宫的递归求解

dirs = [(0,1), (1,0), (0,-1), (-1,0)] #按照东南西北的顺序,给出它与四个方向的差距值。 def mark(maze, pos): ‘‘‘ 用来标记走过的路径。 ‘‘‘ maze[pos[0]][pos[1]] = 2 def passable(maze, pos): ‘‘‘ 检查是否可行 ‘‘‘ return maze[pos[0]][pos[1]] == 0 def find_path(maze, pos, end): mark(maze, pos) if pos == end: print(pos, end=‘ ‘) return True for i in range(4): nextp = pos[0]+dirs[i][0], pos[1]+dirs[i][1] if passable(maze, nextp): if find_path(maze, nextp, end): print(pos, end=‘ ‘) return True return False
栈和回溯法
回溯法在工作中执行两种基本动作:前进和后退。
前进:
后退:

def maze_solver(maze, start, end): if start == end: print(start) return st = SStack() mark(maze, start) st.push((start, 0)) # 0指的是需要从哪个方向开始探索。 while not st.is_empty(): pos, nxt = st.pop() for i in range(nxt, 4): nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1] if nextp == end: print(end, pos, st) return if passable(maze, nextp): st.push((pos, i+1)) # 将原位置和下一个方向存入栈中。 mark(maze, nextp) st.push((nextp, 0)) break
关于这个算法,有两点说明:
3、迷宫问题和搜索
其实迷宫问题,是一类问题的代表,这类问题称为状态空间搜索问题。基本特征:
状态空间搜索:栈和队列
用计算的方法解决问题,根据人们对于问题的认识深度,存在两种不同的处理方法:
搜索法就是一种通用问题的求解方法。但是在搜索的过程中需要缓存一些已知信息,原则上栈跟队列都可以使用,但是不同的选择,会对搜索进展方式有不同的影响。
在前面的迷宫算法里使用的是栈,它的特点是后进先出,因此会产生回溯。
如果使用队列作为缓存,那么实际上是一种从各种可能齐头并进的搜索。这个过程中没有回溯,只是一种逐步扩张的过程。
基于队列的迷宫求解算法

def maze_solver_queue(maze, start, end): if start == end: return qu = SQueue() mark(maze, start) qu.enqueue(start) while not qu.is_empty(): pos = qu.dequeue() for i in range(4): nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1] if passable(maze, nextp): if nextp == end: print(‘Path find‘) return mark(maze, nextp) qu.enqueue(nextp)
上面的算法有一个问题没有解决,就是找到的路径没有存储。如果想只要找到一条路径,必须另行记录与路径有关的信息。可以考虑使用字典结构实现

def maze_solver_queue(maze, start, end): if start == end: return qu = SQueue() mark(maze, start) dic = {} qu.enqueue(start) while not qu.is_empty(): pos = qu.dequeue() for i in range(4): nextp = pos[0] + dirs[i][0], pos[1] + dirs[i][1] if passable(maze, nextp): dic[nextp] = pos # 记录搜索过程中的对象关系key是后一元素,value是前一个元素 if nextp == end: # 根据记录关系,从后往前推,找到路径 p = end while p != start: p = dic[p] print(p) return mark(maze, nextp) qu.enqueue(nextp)
基于栈和队列的搜索过程
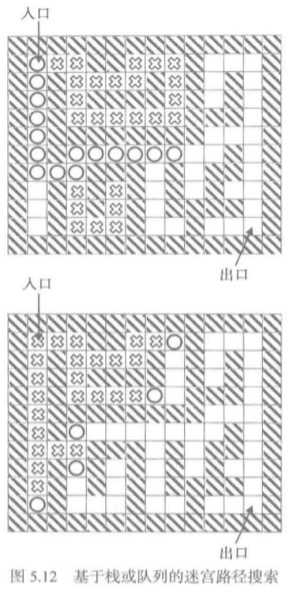
上图中分别是迷宫示例中基于栈和队列的两种不同的搜索路径图。其中栈的特点是,先找一个方向,直到不能再继续的时候,返回最近的那个分叉处,继续探索。因此它是深度优先的搜索。
队列的特点是一步一步搜索,如果有通路就进行前一步探索,不会出现回溯现象。因此它是宽度优先的搜索。
深度和宽度优先搜索的性质
如果一个问题可使用空间搜索方法解决,那是用深度优先还是宽度优先,需要根据具体情况,也就是上面的性质来进行选择。
六、补充
1、与栈和队列相关的结构
双端队列
deque,它允许在两端插入和删除元素。
双端队列的实现方式
python的deque类
python标准库中collections定义的deque类型,提供了一种双端队列的操作,它是采用双链表的技术实现的,但是其中每个链接结点里顺序存储一组元素。
2、问题讨论
问题:对于栈和队列,既然链表能实现统一的O(1),那么为什么还要考虑顺序实现呢?
答:因为计算机的分级缓存结构(参考csapp第1章的存储管理)。如果连续进行一批内存访问是局部的,操作速度就会很快。因此,在考虑程序的效率时,一个重要线索就是对计算机内存使用的局部化。而链接结构的一个特点是,其中结点在内存中是任意分散的,因此,对链表元素的访问是在很多位置的内存单元跳来跳去的,因此它的效率没有顺序表实现的高。
原文:https://www.cnblogs.com/walle-zhao/p/11387310.html