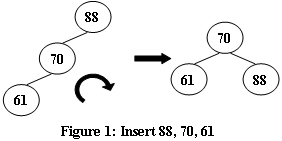
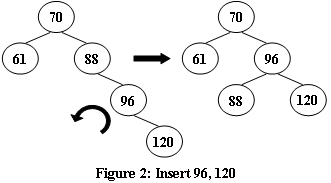
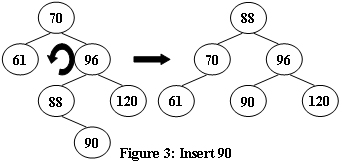
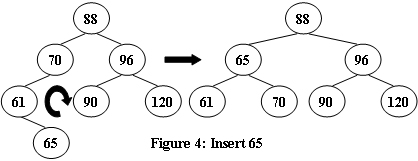
An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.
 |  |
|---|---|
 |
 |
Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.
Each input file contains one test case. For each case, the first line contains a positive integer N (≤ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.
For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YESif the tree is complete, or NO if not.
5
88 70 61 63 65
70 63 88 61 65
YES
8
88 70 61 96 120 90 65 68
88 65 96 61 70 90 120 68 NO
分析:这道题考察AVL树和层序遍历以及完全二叉树
判断是不是完全?叉树,就看在出现了?个孩?为空的结点之后是否还会出现孩?结点不为空的结
点,如果出现了就不是完全?叉树。
AVL树?共有四种情况,这?我把发现树不平衡的那个结点叫做A结点,A发现树不平衡的情况有四
种:
新来的结点插?到A的左?树的左?树
新来的结点插?到A的左?树的右?树
新来的结点插?到A的右?树的左?树
新来的结点插?到A的右?树的右?树
发现不平衡时就需要处理,第1种情况只要简单的右旋,第4种情况只需左旋?下,
第2种情况需要先对A的左?树左旋?下,然后对A右旋,同理第3种情况需要对A的右?树右旋?下,然后对A左旋
1 #include <iostream> 2 #include <vector> 3 #include <queue> 4 #include <algorithm> 5 using namespace std; 6 struct Node 7 { 8 int v; 9 Node *l, *r; 10 Node(int a = -1) :v(a), l(nullptr), r(nullptr) {} 11 }; 12 int n, a; 13 vector<int>res; 14 int getHeight(Node* root) 15 { 16 if (root == nullptr) 17 return 0; 18 return max(getHeight(root->l), getHeight(root->r))+1; 19 } 20 Node* rotateRight(Node* root)//右旋 21 { 22 Node*p = root->l; 23 root->l = p->r; 24 p->r = root; 25 return p;//新的根节点 26 } 27 Node* rotateLeft(Node* root)//左旋 28 { 29 Node*p = root->r; 30 root->r = p->l; 31 p->l = root; 32 return p;//新的根节点 33 } 34 Node* rotateLeftRight(Node* root)//左右旋 35 { 36 root->l = rotateLeft(root->l);//先左旋 37 return rotateRight(root);//再右旋 38 } 39 Node* rotateRightLeft(Node* root)//右左旋 40 { 41 root->r = rotateRight(root->r);//先右旋 42 return rotateLeft(root);//再左旋 43 } 44 Node* Insert(Node* root, int x) 45 { 46 if (root == nullptr) 47 { 48 root = new Node(x); 49 return root; 50 } 51 if (x < root->v) 52 { 53 root->l = Insert(root->l, x); 54 if (getHeight(root->l) - getHeight(root->r) >= 2) 55 root = x < root->l->v ? rotateRight(root) : rotateLeftRight(root); 56 } 57 else 58 { 59 root->r = Insert(root->r, x); 60 if (getHeight(root->r) - getHeight(root->l) >= 2) 61 root = x > root->r->v ? rotateLeft(root) : rotateRightLeft(root); 62 } 63 return root; 64 } 65 bool LevelOrder(Node* root) 66 { 67 bool flag = true;//是不是完全二叉树 68 if (root == nullptr) 69 return flag; 70 queue<Node*>q, temp; 71 q.push(root); 72 while (!q.empty()) 73 { 74 Node*p = q.front(); 75 q.pop(); 76 temp.push(p); 77 res.push_back(p->v); 78 if (p->l != nullptr) 79 q.push(p->l); 80 else if (temp.size() + q.size() != n)//中间出现空节点,不是完全二叉树 81 flag = false; 82 if (p->r != nullptr) 83 q.push(p->r); 84 else if (temp.size() + q.size() != n)//中间出现空节点,不是完全二叉树 85 flag = false; 86 } 87 return flag; 88 } 89 int main() 90 { 91 cin >> n; 92 Node* root = nullptr; 93 for (int i = 0; i < n; ++i) 94 { 95 cin >> a; 96 root = Insert(root, a); 97 } 98 bool flag = LevelOrder(root); 99 for (int i = 0; i < res.size(); ++i) 100 cout << (i > 0 ? " " : "") << res[i]; 101 if (flag) 102 cout << endl << "YES" << endl; 103 else 104 cout << endl << "NO" << endl; 105 return 0; 106 }
PAT甲级——A1123 Is It a Complete AVL Tree【30】
原文:https://www.cnblogs.com/zzw1024/p/11477748.html