二叉树

一、二叉树的基本概念

1.结点的度：结点所拥有的子树的个数称为该结点的度。

2.叶子结点：度为0的结点。

3.分支节点：度不为0的结点。一棵树除了叶子节点外全部都是分支结点。

4.孩子结点、双亲结点和兄弟结点：以图一为例，A是B、C的双亲结点，B、C是A的孩子结点，B、C互为兄弟结点。

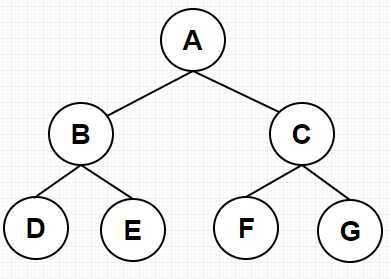
　　　　　　　　　　　图一

5.路径、路径长度：如果一棵树的一串结点n₁、n_2，…，n_k有如下关系，结点n_i是ni+1的父节点（1≤i≤k），就把n₁、n_2，…，n_k称为一条由n₁到n_k的路径，这条路径的长度为k-1；

例如：图二中n₁到n₃有一条路径，则该路径的长度为2

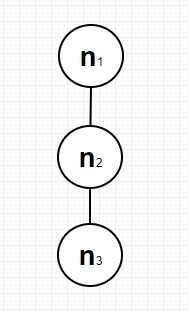
 　　　图二

6.结点的层数：规定树的根节点的层数为1，其余结点的层数等于它的双亲结点的层数+1。

例如：图一中，结点A的层数为1，结点B和结点C是结点A的孩子结点，则结点B和结点C的层数均为2，结点D是结点B的孩子结点，则结点D的层数为3。

7.树的深度：树中所有结点的最大层数。例如：在图一中，树的最大层数为3层，则树的深度为3。

8.树的度：树中各结点的最大值称为树的度，叶子结点的度为0；例如：在图一中，A的度为2，B、C的度为2、D、E、F、G为叶子结点，度为0，则该树的度为2。

9.满二叉树：在一棵树中，所有的分支节点都存在左子树和右子树，且所有的叶子结点都在同一层，则该树为满二叉树。

　　如图：图一为满二叉树，图三不为满二叉树

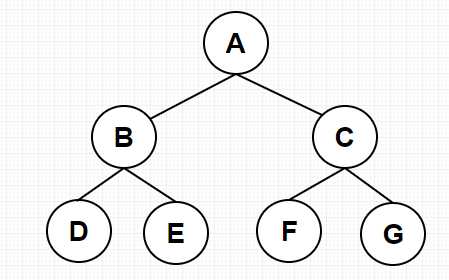
 　　　　　　　　　　图一　　　　　　　　　　　　　　　　　　　　　  图三

10.完全二叉树：在一颗二叉树中，出最后一层外，其余层都是满的，并且最后一层或是满的。或是在右边缺少连续若干个结点。满二叉树是完全二叉树的特例。

例如，上图图一、图三均为完全二叉树。

二、二叉树的性质

1.一棵非空的二叉树第i层上最多有2^i-1个结点。

2.一棵深度为k的二叉树中，最多有2^k-1个结点，最少有k个结点。

3.一棵非空的二叉树度为0的结点总是比度为2的结点多一个。

4.具有n个结点的完全二叉树的深度为[log₂n]+1（[]为向下取整）

5.对于完全二叉树中有n个结点，对于编号为i的结点，若该节点有左子树，则左子树的编号为2i；若该节点有右子树，则右子树的编号为2i+1；若n为奇数则每个分支既有左子树又有右子树，若n为偶数，则编号最大的分支结点只有左子树。

三、二叉树遍历

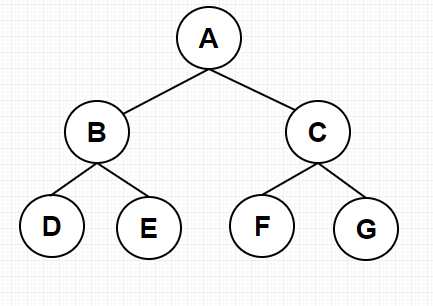
 　　　　　　均以该图为例

1.前序遍历（根左右）

　　若二叉树为空，遍历结束。否则，第一步，访问根结点；第二步，先遍历根结点的左子树；第三步，遍历根结点的右子树。

　　上图中，先访问结点A，输出A，遍历结点B，输出B,结点B遍历结点D，结点D为叶子结点，输出D，返回结点B，遍历结点E，结点E为叶子结点，输出E，返回结点B，结点B的左右结点均遍历过，返回结点A，结点A已经访问过，为访问结点A的右子树即结点C，输出C，遍历结点C，遍历结点F，结点F为叶子结点，输出F，返回结点C，遍历结点G，结点G为叶子结点，输出G，返回结点C，结点C访问过，返回结点A，结点A的左右子树均遍历过，遍历结束。

　　上图前序遍历的顺序为：ABDECFG。

2.中序遍历（左根右）

　　若二叉树为空，遍历结束。否则，第一步，遍历根节点的左子树；第二步，访问根节点；第三步，遍历根结点的右子树。

　　上图中，先访问结点A，结点A存在左子树，遍历结点A的左子树结点B，结点B也存在左子树，遍历结点E，结点E为叶子结点，输出结点E，返回结点B，输出结点B，结点B的右子树为访问过，访问结点B的右子树（结点E），结点E为叶子结点，输出E，返回结点B，jiedianB的左右子树均访问过，返回结点A，输出A，结点A的右子树为访问过，遍历结点C，遍历结点F，结点F为叶子结点，输出F，返回结点C，输出C，访问结点C的右子树，结点G为叶子结点，输出G，返回C，返回A，结点A的左右结点均访问过，遍历结束。

　　上图中序遍历顺序为：DBEAFCG

　　上图前序遍历的顺序为ABDECFG。

3.后序遍历（左右根）

　　若二叉树为空，遍历结束。否则，第一步，遍历根节点的左子树；第二步，遍历根节点的右子树；第三步，访问根结点。

　　上图中，先访问结点A，遍历结点B，结点B遍历结点D，结点D为叶子结点，输出结点D，返回结点B，结点B的右子树未访问过，遍历结点E，结点E为叶子结点，输出E，返回结点B，结点B的左右结点均遍历过，输出B，返回结点A，未访问结点A的右子树即结点C，遍历结点C，遍历结点F，结点F为叶子结点，输出F，返回结点C，遍历结点G，结点G为叶子结点，输出G，返回结点C，结点C的左右结点均访问过，输出C，返回结点A，结点A的左右子树均遍历过，输出A，遍历结束。

　　上图前序遍历的顺序为DEBFGCA。

四、二叉排序树（二叉查找树）

　　二叉查找树或者是一棵空树，或者满足以下条件：

　　a.若左子树不为空，左子树上所有结点的值均小于它的根节点的值；

　　b.若右子树不为空，右子树上所有结点的值均大于它的根节点的值；

　　c.左右子树也分别为二叉查找树。

　　例如，图四就是一棵二叉查找树

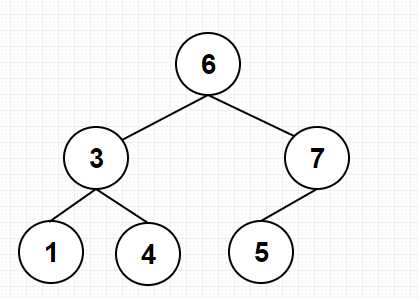
 　　　　　　　　　　　　　　　　　 图四

五、二叉树的最大距离

　　二叉树结点最大距离为左子树距根节点的最大距离+右子树距根节点的最大距离。

二叉树

原文：https://www.cnblogs.com/shuo2018/p/11478249.html