首先，复习一下欧拉函数(https://www.cnblogs.com/hnoi/p/10992072.html)：
在算术基本定理中，
1~N中与N互质的数的个数成为欧拉函数：
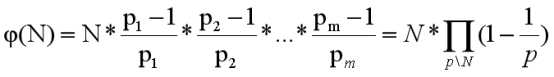
费马小定理：
若p是质数，则对于任意整数a，有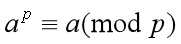
。
欧拉定理：
若正整数a,n互质，则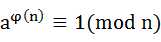 
。
证明：
设n的简化剩余系是{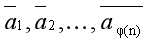
}
对任意ai,aj,有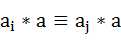
。
因为a,n互质，所以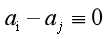
。当
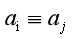时，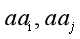
代表不同的同余类。
因为简化剩余系关于模n乘法封闭，故也在剩余系集合中。
综上所述，
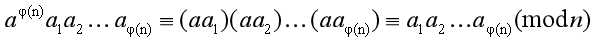
因此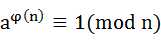
。
证毕。
原文：https://www.cnblogs.com/hnoi/p/11481714.html