大概就是找到每个区间里最长的序列使得其中没有重复
思路:
因为知道可以用ST表维护但不是简单的最大值,所以第一个思路是
用dp[i][j]表示正常的ST表,但是其值表示以点i结尾的最大完美序列长度
为什么能想到这个思路?原因非常简单,我们已经知道ST表正常情况下
只能用来维护最大最小值,所以我们必须把序列长度往最大最小这个思路里靠,
就有了存储以i结尾序列长度最大值的存储方法
但是我们会发现有这样一个问题:
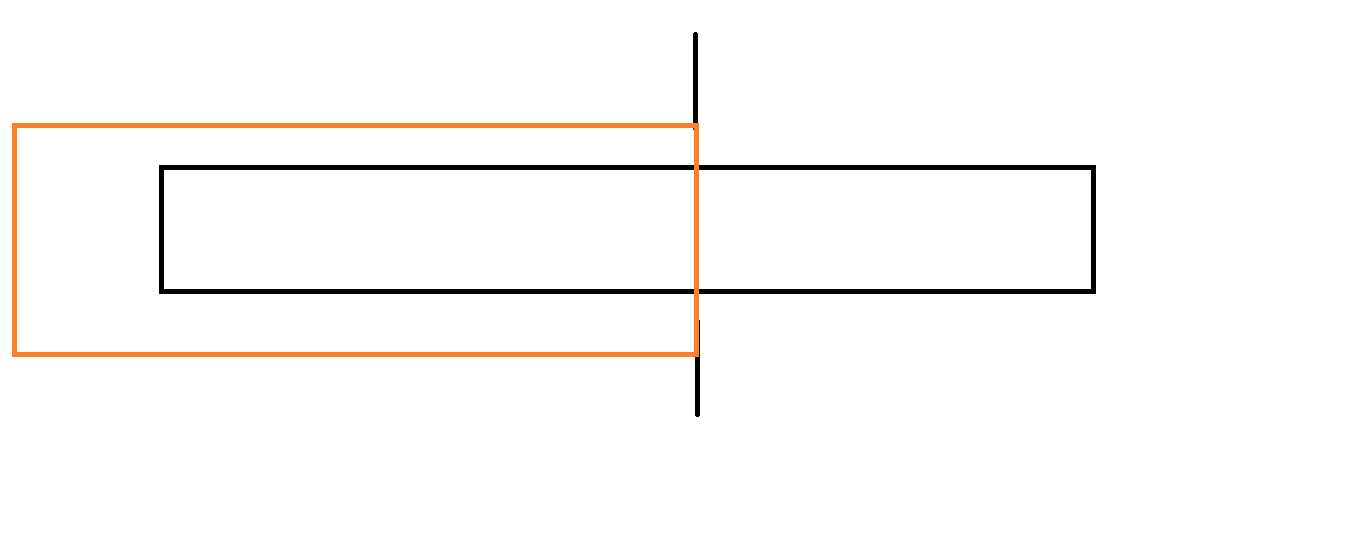
这个图里的竖线表示黑色区间里以i结尾的所有完美序列中最长的序列的那个i,
我们记这个点是p
(也就是这段区间所有点内以其结尾的最长完美序列的结尾点)
但是如果橙色区间内是点p结尾的最长完美序列覆盖到的地方,
我们可以发现它已经超过了待求区间的范围
怎么办???
解决问题首先要明确问题的范围
所以我们用f[x]表示在整个数组中x之前出现的上一个与其值相同的点得位置
比如说 点x对应的值是5 f[x]就是在x之前上一个5的位置
这样我们就明确了什么时候会出现第一部分的情况
从f数组的思路 我们可以得到一个last数组 last[x]表示以x结尾的最长完美序列的起点位置
这样我们就可以用st[i]表示以i结尾的最长完美序列的长度
很明显st[i]=i-last[i]+1
所以初始化这两个数组(f数组在代码中不需要)只需要初始化last
为了初始化last 我们借助尺取法的思路
一开始使用两个指针l,r都指向位置n,再开一个book数组记录已经出现过哪些数
注意book一定要开map 因为原序列有负数!!!!!!(哭唧唧qwq)
所以我们每次将l向前移动一个位置 扫描到一个数
如果这个数没有出现过 标记该数已经出现过
如果这个数已经出现过
从后向前移动右指针r一直移动到l-r序列中没有重复数,
所有移动过去的数标记他们的last[i]=l+1
如果l扫描到1但是r没有扫描到1,从r当前位置往前扫描r标记book[r]=-1,
表示r结尾的完美序列起点一直可以到第一个数
这个方法的正确性证明如下:
因为每次扫描左指针的时候都没有重复数字,
所以直到找到重复数字为止(l+1)-r这段区间都没有重复数字
也就是说从r一直往回找到与a[l]重复的那个位置(a数组表示原序列)为止
中间扫过的所有数到l+1的位置都没有重复数字
但它不能再往前扫描到l 因为从这个正在扫过的数到l+1中间经过了那个与a[l]重复的位置
如果它再扫描到l 这个以l开始以正在扫描到的这个r和重复位置中间的某个数结尾的序列必然经过那个重复位置
(因为r>那个与a[l]重复位置的编号)
这样我们就可以在O(2n)的复杂度内初始化last数组
同理,我们可以在O(n)的复杂度内初始化st数组
同时注意dp数组存储的不是原序列而是st即可
其实初始化last和st还有一个方法但我不会(逃)
但是我们现在只是明确了问题的范围
所以为了解决以某些点结尾的序列的起点在待查询的区间外,
我们观察last数组 很明显last数组是单调递增的
证明如下:
假设现在存在一段区间,其中该区间前两个点标记为l1,l2(l1<l2),后两个点标记为r2,r1(r2<r1)
其中last[r1]=l1,last[r2]=l2
大概就是存在这种一段完美序列完整包含了另一段完美序列的情况
因为对于完美序列(l2,r2)一定有且只有一个l1(否则(l2,r2)就不是以r2结尾的最长完美序列,即last[r2]!=l2)
但是由于(l2,r2)包含在(l1,r1)中
所以完美序列(l2,r1)一定也有且只有一个l1
所以(l1,r1)中有两个l1
与(l1,r1)是完美序列矛盾,所以:
对于任意的(r2,r1)(r2<r1),两点为结尾的完美序列分别的左端点(l2,l1)一定满足l2<l1.
又因为l1=last[r1] l2=last[r2] l1<l2 r1>r2 所以last满足单调递增。
因为单调递增 而又因为第一部分的问题
所以我们可以二分一个点mid 使得以mid及其左边的点为结尾的完美序列的
左边界都在不在待查区间内 其右侧点为结尾的完美序列的左边界都在待查区间内
其实就是这样
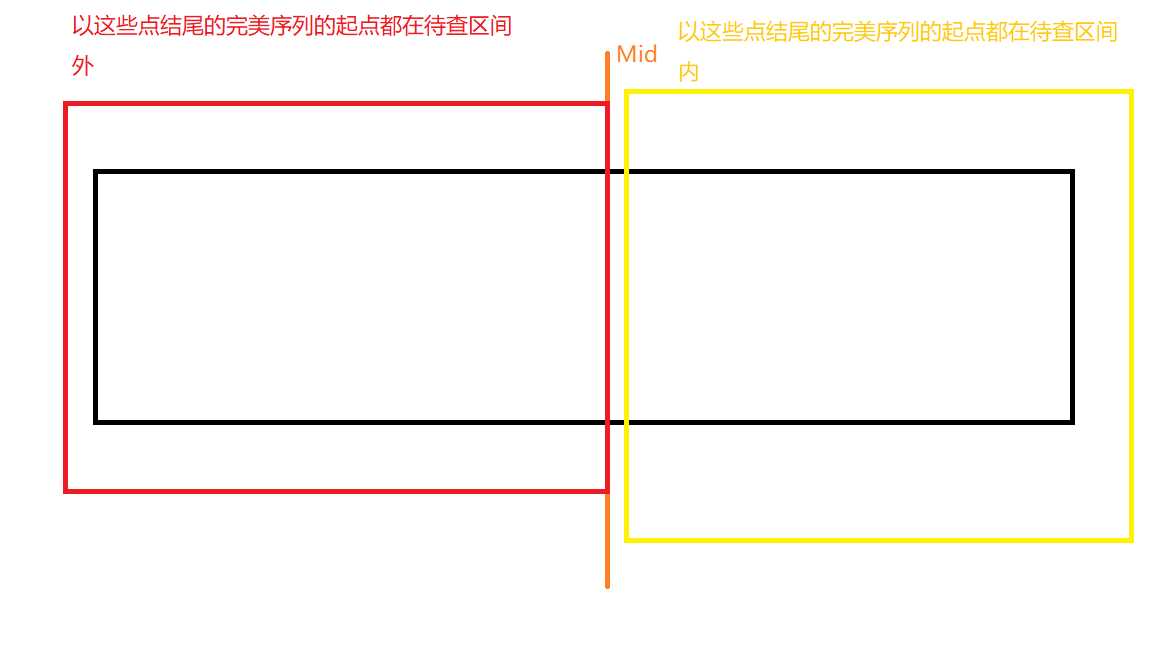
这样对于一个区间完美序列的长度我们可以分为两个部分计算:
mid及其左侧的部分,设待查区间左端点为l,则ans=max(x-l+1),
其中x是mid及其左侧的点;
这样做的正确性在于 因为last[x]<l 所以l--x这一段肯定在以x结尾的完美序列里
也就是说它也是完美序列;
又因为mid是离l最远满足last[x]<l的点 所以ans=mid-l+1;
对于mid右侧的部分,ans=ask(mid+1,r),其中ask用ST表维护区间最大值;
综上,对于二分出的分界点mid,有ans=max(mid-l+1,ask(mid+1,r));
也就是说这个题的思路大概是这个样子:
(1)通过观察到“完美序列的左端点不在待查区间内”的问题,明确该问题的
范围(建立last数组);
(2)利用分类讨论的思想,将“完美序列的左端点不在待查区间内”的情况
和“完美区间内的左端点在待查区间内”的情况分别处理;
(3)找到两种情况的分界线(二分mid);
(4)讨论左端点不在待查区间内的情况,根据完美序列的性质(完美序列的子序列
一定是完美序列)推出mid及其左侧点的求解方法;
(5)讨论左端点在待查区间内的情况,将问题转化为研究过的问题(区间最大值),
根据所求问题及已有的条件(last数组)初始化出st数组作为ST表的初值;
(6)综合两部分答案,得出所求结果。
放代码:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<map> #define int long long using namespace std; int n,m,a[2000500],dp[2000500][65],last[2000500],st[2000500]; map<signed,int> book;//注意盈利值有可能是负数,所以利用带符号的signed类型作为下标(坑了我所有的分qwq) void init() { int l=n,r=n; memset(last,-1,sizeof last); memset(st,-1,sizeof st); for(l=n;l>=1;--l)//尺取法初始化last数组 { if(book[a[l]])//已经扫描过这个点 { while(a[r]!=a[l])//向前扫描到重复的点 { last[r]=l+1;//中间所有扫描过去的点标记以它结尾的完美序列的起点为l+1 book[a[r]]=0;//这个值现在不在序列中 --r; } last[r]=l+1;//标记最后一个重复的点 --r; } book[a[l]]=1;//标记这个值进入了序列 } for(int i=1;i<=n;i++) { if(~last[i])st[i]=i-last[i]+1; else st[i]=i; } for(int i=1;i<=n;i++)dp[i][0]=st[i];//注意应当以完美序列的长度作为初值 for(int j=1;(1<<j)<=n;j++) for(int i=1;i+(1<<j)-1<=n;i++) dp[i][j]=max(dp[i][j-1],dp[i+(1<<j-1)][j-1]); } int ask(int l,int r) { int k=log2(r-l+1); return max(dp[l][k],dp[r-(1<<k)+1][k]); } signed main() { // freopen("in.txt","r",stdin); // freopen("out.txt","w",stdout); scanf("%lld%lld",&n,&m); for(int i=1;i<=n;i++)scanf("%lld",&a[i]); init(); // for(int i=1;i<=n;i++)printf("%lld ",last[i]); // puts("\n"); int x,y; for(int i=1;i<=m;i++) { scanf("%lld%lld",&x,&y); ++x; ++y; if(last[y]<x) { printf("%lld\n",y-x+1); continue; }//如果所有的点都满足以该点结尾的完美序列起点不在待查区间内,直接退出二分 if(last[x]==x) { printf("%lld\n",ask(x,y)); continue; }//同理,所有起点都在待查区间内 int ll=x,rr=y,flag=-1,mid=x; while(ll<rr-1) { mid=(ll+rr)>>1; if(last[mid]>=x)rr=mid-1; else ll=mid; } if(last[mid]<x&&last[mid+1]>=x)printf("%lld\n",max(mid-x+1,ask(mid+1,y))); else if(last[ll]<x&&last[ll+1]>=x)printf("%lld\n",max(ll-x+1,ask(ll+1,y))); else if(last[rr]<x&&last[rr+1]>=x)printf("%lld\n",max(rr-x+1,ask(rr+1,y)));//二分查找mid } return 0; } /* 5 1 -4 5 -9 3 4 1 2 */
本题思维难度较大,希望大家明白之后自行再写一遍。
原文:https://www.cnblogs.com/qxds/p/11479803.html