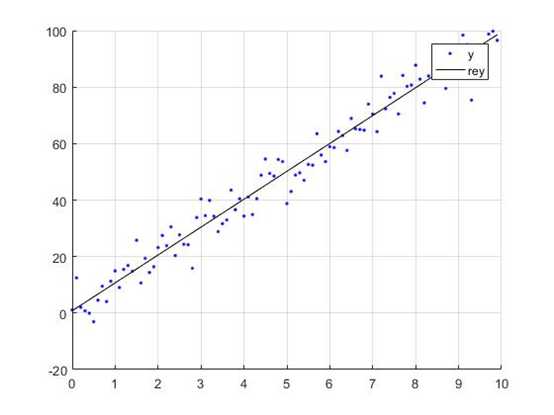
背景:我们有一系列的点(x,y),如下图所示,实际上这就是一个y=10*x的一元一次曲线,再加上一个随机误差得到的数据。
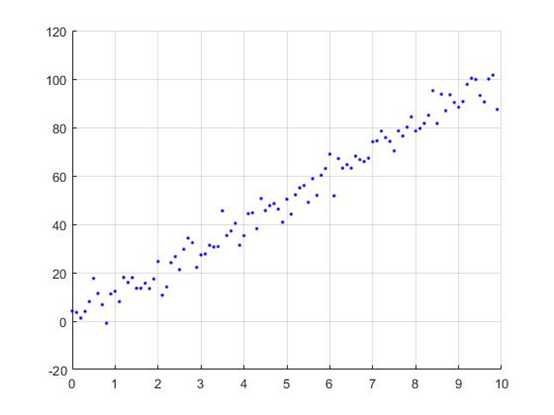
我们想用一个线性方程来拟合它y=a*x+b
为了达到最好的拟合效果,我们应该让
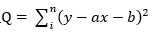
最小。(y是原始值)。
对上式求导
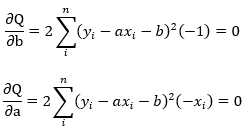
对上式稍微整理以下,使用克莱姆法则,得
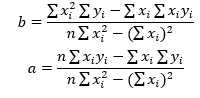
矩阵的表达形式
如果我们推广到更一般的情况,假如有更多的模型变量x^1, x^2,…, x^n(注意:x^1是指一个样本,x_1是指样本里的一个模型相关的变量),可以用线性函数表示如下:
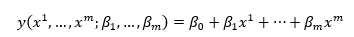
对于n个样本来说,可以用如下线性方程组表示:
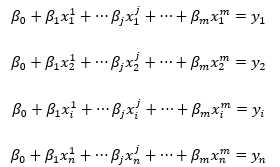

注意事项
经典的最小二乘法使用起来够简单粗暴,计算过程也不复杂。但是一个致命的问题就是其对噪声的容忍度很低。试想一下,如果前面我们得到的总采样数据为100个,但是里面有几个误差比较大的数据,这就是噪声了。如果不采取一些手段对这几个噪声样本进行处理,最后拟合的效果肯定不是很好。
对于噪声的处理,比如有加权最小二乘等方法,后续有时间跟大家再讲讲
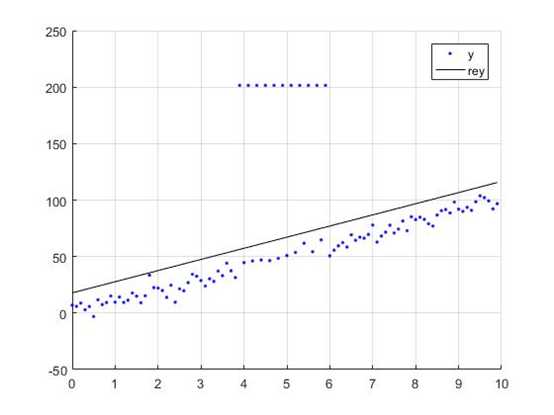
我们加入更大一点的噪声,发现这时候拟合的效果就不是很好,噪声直接把拟合曲线给带偏了。
下面是多项式拟合的结果
免费获取源码,请关注公众号 洛水梅家。

原文:https://www.cnblogs.com/xutopia/p/11488894.html