凸优化问题 Convex Problems

凸优化的广义定义

广义上讲，目标函数是凸函数，且相关约束是凸集约束，那么这个问题就称为凸优化。

但实际上我们经常遇见的凸优化问题范围会更小一点。

一般优化问题的描述

\[ \begin{aligned} min \qquad & f_0 (x) \ s.t \qquad & f_i (x) \leq 0, \quad i=1,...,m \ & h_i(x) = 0, \quad i=1,...,p \end{aligned} \]

下面介绍一下与上面式子相关的名词

名词介绍

1. 优化变量 Optimization Variable： \(x\in R^n\)
2. 目标函数/损失函数(objective function/cost function)：\(f_0 : R^n \rightarrow R\)。当是最大化某个函数时，对应的函数可以成为效用函数（utility function）。
3. 不等式约束（Inequlity constant）：\(f_i(x) \leq 0\)
4. 等式约束（equlity constant）：\(h_i(x)=0\)
5. \(m=p=0\)时，则问题就变成无约束问题了（unconstanted）。
6. 优化问题的域(domain)：
   \[D= \bigcap^m_{i=1}dom \ f_i \cap \bigcap^p_{i=1}h_i\]
7. 可行解（feasible set）
   \[ \begin{aligned} & x\in D 为可行解，则 \ &f_i(x) \leq 0 \qquad i=1,...,m \ &h_i(x) =0 \qquad i=1,...,p \\end{aligned} \]
   记：
   \[X_f = \{x为可行解\}\]
8. 问题的最优值（optimal value）
   \[ \begin{aligned} p^* = inf \{f_0(x)|x \in X_f\} \end{aligned} \]
9. 最优解(optimal point/solution)
   \[若x^*可行，且f_0(x^*)=p^*\]
10. 最优解集（optimal set）
    \[X_{opt}=\{x|x \in X_f, f_0(x)=p^*\}\]
11. \(\epsilon\)次优解集(\(\epsilon -suboptimal set\))
    \[X_{\epsilon} = \{x|x\in X_f , f_0(x)\leq p^* + \epsilon \}\]
12. 局部最优解集（locally optimal）
    

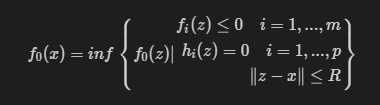
凸优化【4 凸优化问题的描述及基本概念】

原文：https://www.cnblogs.com/shenhaojing/p/11492621.html