感性的理解,主席树就是多个阶段下(即可保存多个版本)的多棵线段树(可以是普通线段树也可以是权值线段树)。
一、权值线段树
普通线段树相信大家都会,这里先简述一下权值线段树。
顾名思义,权值线段树的每个节点带的[l,r]表示的是权值区间l~r,而不是像普通平衡树上那样表示在序列上的第l个位置~第r个位置。而每个节点的val值表示该权值区间内有多少个数。比如对于1,4,1,6,4,4,2这样一个序列,可以表示为下图:
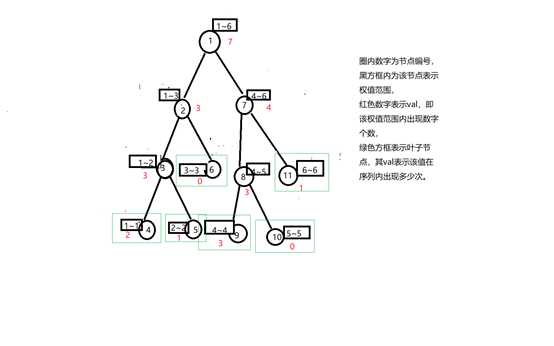
对于插入操作,直接从根节点往下找到所有权值范围包括k的节点,将其val++,一直到叶子节点。
对于查询操作,如查询第k小的数,即从根节点开始,若 左子树的val<=k ,就往左子树继续查找,否则将 k-=左子树的val 并往右子树查找(显然该范围的第k小就是其右子范围的第 k-tre[tre[x].ls].val 小)。
应该是比较好理解的。
但是,有一个很严重的问题,比如说1,10^6,10^7这样一个序列,明明只有三个元素,但是对于权值线段树,我们是要开 2*(10^7) 的节点的,显然空间上是无法接受的。怎么办呢?
这里讲的是 离散化+动态开点。
首先离散化,就是用每个权值在序列中的排名来代替该权值在序列中的位置。
其次是动态开点。在普通线段树中,我们建树、插入、查询的时候都是直接走的 rt<<1 或者 rt<<1|1 ,但是我们发现,有些节点是不需要的,比如说我们插入一个5,走到权值区间 [4,6] 的时候,两个子区间 [4,5] ,[6,6] 中,显然就不需要建 [6,6] 这个节点。那怎么代码实现呢?下一步需要走到那个区间,我们就直接走 tre[rt].ls(或.rs) (如果没有该节点就新建一个)。
上代码:
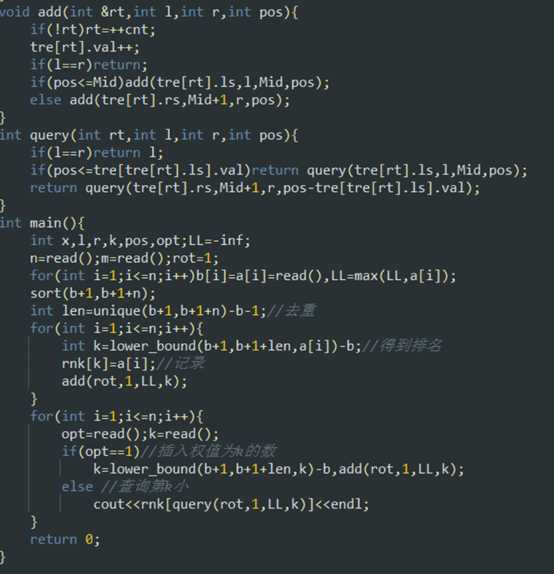
代码很短吧。
二、主席树(正题)
主席树最经典的模板题:静态区间第k小。(https://www.luogu.org/record/23797386)
首先学习如何建主席树。
如果用最暴力的做法,显然,对于每一个阶段开一个线段树就可以了,然后开个root数组来记录每个阶段的线段树的根。
比如说依次输入5,1,3,离散化后为3,1,2。如下图:
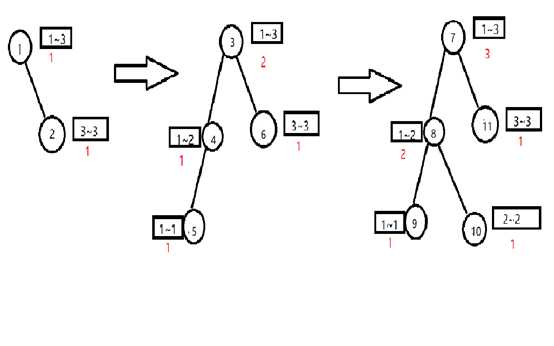
但是显然,空间是无法接受的——我们需要开[maxn][maxn<<2]的数组。
我们可以发现,所有的阶段上的树是有相同的部分了。比如说第一棵树的2,,第二棵树的6,和三棵树的11,所以我们可以直接把3,4号节点的右儿子直接设成2,同理8的左儿子可以直接设成5,这样就节省了很多空间。
然后直接讲讲区间第k小,这里就需要用到主席树的一个类似前缀和的思想。你会发现,如果把每两棵树上的所有对应节点的val相减,最终也能得到一颗权值线段树,而这棵权值线段树所含的数即是这两个阶段之间输入的数即位置区间 [l,r] 上的数(手动模拟,就不画图了),然后直接对这棵得到的权值线段树做第k小就可以了。
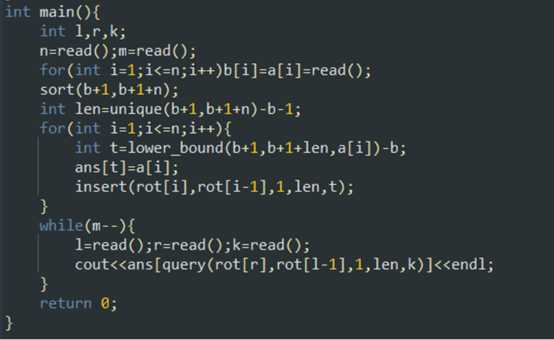
直接上代码吧:
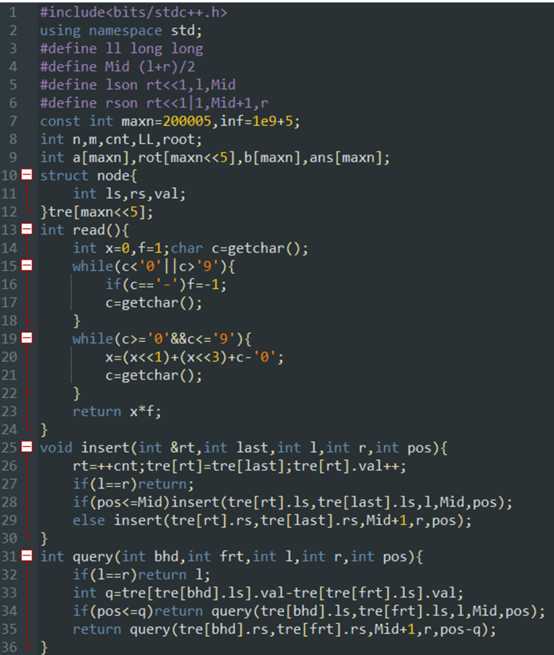
那就到这了,谢谢阅读。
原文:https://www.cnblogs.com/Zikual/p/11494264.html