『YQOI2019』失昼城的守星使 题解

本场比赛的最后一题，不过好像并没有任何防AK的作用。

至于YQOI,那是没前缀名看了不顺眼。

树链剖分模板题？有点像。

题目大意

给定一棵树和每个点的初始状态（标记或不标记），每次修改一个点的状态（状态取反）或询问树上所有标记点到\(u->v\)的简单路径的最短距离之和。

以下是数据范围：

无脑暴力

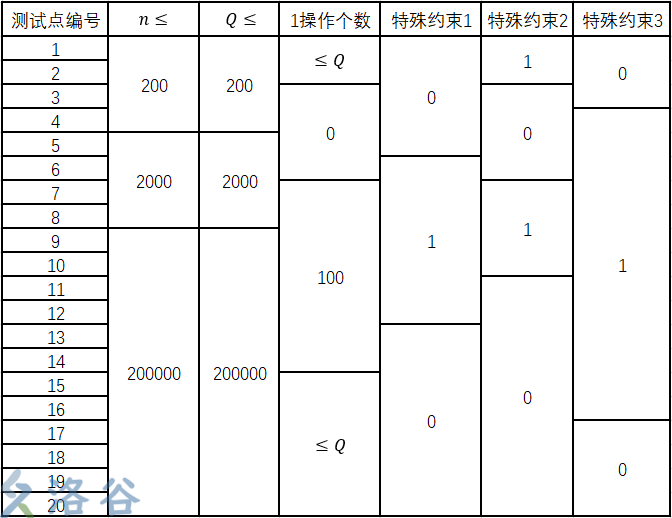
我们把矛头盯准前4个点。

\(n,m\leq 200\)，这意味着什么？

直接按照题意模拟，先找出\(u->v\)简单路径上的所有点并标记，然后以每个点为根节点，找到最近的被标记的点，这个点显然最优，记录累加答案即可。

时间复杂度：\(O(n^2m)\)期望得分：\(20\).

不过由于数据比较水，放过了第\(7,8\)两个全特殊约束的点，可以拿到\(30pts.\)

高端暴力

解决了\(n,m\leq 200\)的点，我们可以看到接下来的数据为\(n,m\leq 2000\).

通俗易懂的讲我们要在\(O(nm)\)时间内完成答案。

在分析一下，不难发现，对于每次询问我们要做到\(O(n)\)的时间复杂度。

我们枚举链上的每个点，当枚举到点\(x\)时，考虑有哪一些标记点的最短距离是到\(x\)的。

容易发现去掉和它相邻的点所囊括的范围之后包含的点即为\(x\)点的范围。

可以这样理解：

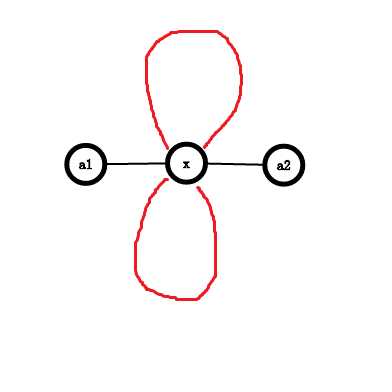
图中红圈内的点到链上的最短距离都是到\(x\)。

设\(f[x]\)表示以\(x\)为根的所有标记点到\(x\)的距离，\(num_x\)表示以\(x\)为根的子树有多少个有标记，转移是显然的：

\[f[x]=num_y*val_{x,y}+\sum_{y\in son\{x\}}f[y].\]

累加答案即可。

时间复杂度\(O(nm)\)，期望得分\(40\).

定链求和

这里针对特殊约束2.

不难发现，如果询问\(u->v\)不改变的话，我们只需要针对每次修改更新答案即可。

修改点\(x\)时，我们需要快速找到\(u->v\)路径上的最近点。

如果以\(u\)为根的话，那么我们要找的点就是\(LCA(x,v)\).

时间复杂度：\(O(nlogn+mlogn)\),期望得分：\(30\).

树链求和

这里针对特殊约束1.

树退化成了一条链，我们只要在这条链上寻找答案即可。

我们不妨把树链抽象成一个数列，

询问\(l->r\)时，我们只需要求出\(1->l\)中的点到\(l\)的距离和加上\(r->n\)中的点到\(r\)的距离和就行了。

这里仅考虑到\(l\)的部分（到\(r\)的部分同理）。

发现\(dis(i,l)=dis(i,n)-dis(l,n)\),

求和时，\(ans=\sum_{i=1}^ldis(i,n)-num_{1->l}*dis(l,n)\).

显然\(\sum_{i=1}^ldis(i,n)\)和\(num_{1->l}\)都是可以用某些单点修改区间求和的数据结构来维护的。

那么这几分就拿到了。

时间复杂度：\(O(nlogn+mlogn)\),期望得分：\(35\).

不带修改的离线做法

做到这里，应该就会有些眉目了。

发现有些点的1操作数量不会很多，只要每次修改后暴力重构，我们就只要处理询问部分。

考虑优化"高端暴力"，我们发现处理这种暴力的时候每次都会重复累加好多点。

事实上，我们可以直接预处理暴力时所求的范围。

考虑倍增，设\(g[x][j]\)表示\(x\)的\(2^j\)祖先的\(f\)值去掉\(f[x]\)所剩下的值，\(G[x][j]\)表示x到祖先的同刚才那个区域到这条链上的距离。

在不考虑修改的情况下，\(f[x]\)是可以事先求出来的。

在从\(x\)跳上\(x\)的\(2^j\)祖先\(anc\)的过程中，我们只要累加上\(G[x][j]\)即可，对于外面的世界，用\(g[x][j]\)处理就行了。

时间复杂度：\(O(k(nlogn+mlogn))\)其中\(k\)是修改数,

期望得分：\(60\).（有点小卡常）。

Part A

假设所求路径\(u,v\)的\(LCA(u,v)=lca\).

我们考虑\(lca\)子树内所有的点对答案的贡献。

前面我们说到倍增是没有办法修改点的，这里我们尝试树链剖分。

首先要清楚我们所维护的值,不妨设点有没有被标记为数组\(tag[i]\).显然

\[f[x]=\sum_{tag[i],LCA(x,i)==x}dep[i]-dep[x]=\sum_{tag[i],LCA(x,i)==x}dep[i]-num_i*dep[x].\]

具体可以参考树链部分。

显然\(\sum_{tag[i],LCA(x,i)==x}dep[i]\)和\(num_i\)是可以用欧拉序加上数据结构维护的。

这意味着我们可以在\(logn\)时间内算出\(f[x]\)。

再考虑上面倍增所说到的\(g\)。

这里我们设\(g[x]\)表示\(f[x]\)减去它的重儿子的\(f\)值。

分析一下每次修改的时候我们需要更新哪些点的\(g\)值。

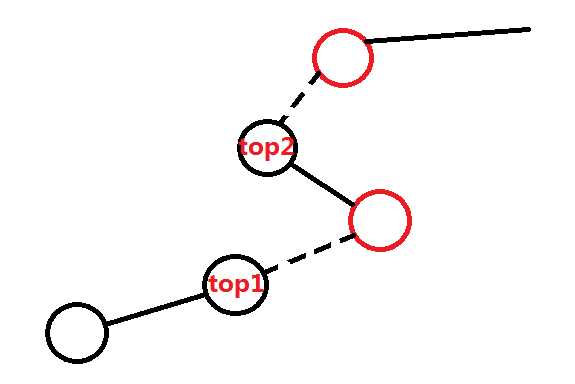
图中虚线代表轻链，实线代表重链。

显然那些红色圈的点才需要更新\(g\)值。

这些点都是某个点\(x\)的\(top[x]\)的父亲节点，易得这样的点有\(logn\)个，是可以做到更新的。

更新完成以后，我们尝试着求答案。

先考虑\(u->lca\)的部分。

如果\(u\)要往上跳到\(fa[top[u]]\)的话，我们的任务就是累加这一部分的和。

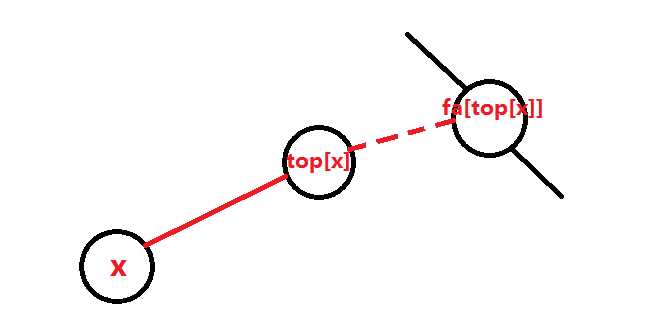
容易发现，当我们跳到点\(x\)时，我们若要跳到\(top[x]\)，就要累加\(x->top[x]\)的这一条链上的\(g\)值。

而要从\(top[x]\)跳到\(fa[top[x]]\)时,

由于\(top[x]\)是轻儿子，我们答案应该要累加\(f[fa[top[x]]-f[top[x]]-num_{top[x]}*val_{top[x],fa[top[x]]}.\)

我们可以惊喜的发现，利用\(f\)和\(g\)可以做到以上所有操作。

这样的时间复杂度为\(O((n+m)log^2n)\).也可以过特殊约束3.

期望得分:\(65\)，加上无脑暴力可以拿到\(80pts\).

Part B

接下来我们要考虑\(lca\)以外的部分,这部分的所有点到这条链上的最短距离都是到\(lca\).

不妨设\(lca\)外面的某个点为\(x\)。

显然\(dis(x,lca)=dep[x]+dep[lca]-2*dep[LCA(x,lca)].\)

那么这部分答案就为

\[\sum dep[x]+num*dep[lca]-2*\sum dep[LCA(x,lca)].\]

前一部分是很好求的，至于\(\sum dep[LCA(x,lca)]\)这部分我们依旧用类似的办法。

为了方便描述，设\(LCA(x,lca)=Lca.\)

往上跳的时候，我们把之前\(g[x]\)所维护的值换为\(num_x*dep[x]\).

我们依旧可以用同样的方法向上跳。

\(g[x]\)换掉了，同样这里的\(f[x]\)也要换掉。

搬回刚才的图，我们发现，从\(top[x]->fa[top[x]]\)的过程中，我们少掉的是\(fa[top[x]]\)的子树去除\(top[x]\)的子树这部分。

那么我们累加的答案就应是\((num_{fa[top[x]]}-num_{top[x]})*dep[fa[top[x]]\).

于是这一部分就做完了。

时间复杂度：\(O((n+m)log^2n)\)，期望得分\(100\).

Summary

• 由于本题需要修改点的标记，我们考虑树链剖分。

• 定义四个树状数组（其他数据结构也行）\(A,B,C,D\).
  • \(A_x\)表示以\(x\)为根的子树有多少个标记点。
  • \(B_x\)表示以\(x\)为根的子树所有标记点的深度和。
  • \(C_x\)表示以\(x\)为根的子树去掉其重儿子为根的子树所形成的范围中的标记点到\(x\)的距离和。
  • \(D_x\)表示以\(x\)为根的子树去掉其重儿子为根的子树所形成的范围中的标记点的数量乘以\(dep[x]\).
  • 换成表达式的话：\(A_x=num_x,B_x=A_x*dep[x],D_x=(A_x-A_{son[x]})*dep[x].\)
  • 显然对于一次修改，\(A,B\)只需修改一次，\(C,D\)要修改\(logn\)次。
• 定义四个函数\(f_x,g_x,F_x,G_x\)(不需要维护)
  • \(f_x\)表示以\(x\)为根的子树中所有特殊点到\(x\)的距离和。显然\(f_x=B_x-A_x*dep_x.\)
  • \(g_x\)表示以\(x\)为根的子树去掉其重儿子为根的子树所形成的范围中的标记点到\(x\)的距离和。显然\(g_x=C_x.\)
  • \(F_x\)表示以\(x\)为根的子树所有标记点的数量乘以\(dep_x\)。显然\(F_x=A_x*dep_x.\)
  • \(G_x\)表示以\(x\)为根的子树去掉其重儿子为根的子树所形成的范围中的标记点的数量乘以\(dep[x]\)。显然\(G_x=D_x.\)
  • 可以发现，以上每一个函数至少可以在\(logn\)内求出。
• 在\(lca\)子树内的部分
  • 如果要从\(x\)跳到\(fa_x\)，且\(x\)是\(fa_x\)的重儿子，直接加上\(g_x\)即可。
  • 面对一条链上的点，所有点的父亲的重儿子都是该点，则可以直接加上\(\sum g_x\)。
  • 对于一条链上的\(top\)点，它是它的父亲的轻儿子，所以我们应该加上\(f_{fa_x}-f_x-A_x*val_{x,fa_x}\)。
  • 值得注意的是，当你从\(u->lca\)和\(v->lca\)跳完之后，我们会多加上一个\(f_{lca}\)，所以答案应该减去\(f_{lca}\)，在从\(u,v\)开始往上跳时，我们需要加上\(f_u,f_v\)，即\(u,v\)的子树部分对答案的贡献。
• 在\(lca\)外的部分
  • 对于从\(lca\)以外的部分，每个点到链上的最短距离都是到\(lca\)。
  • 从前面我们得知，所需要加的答案为\(\sum dep[x]+num*dep[lca]-2*\sum dep[Lca]\)。
  • 也就是\((B_{root}-B_{lca})+(A_{root}-A_{lca})*dep[lca]-2*\sum dep[Lca]\)。
  • 处理\(\sum dep[Lca]\)时，注意到\(Lca\)都是\(lca\)到\(root\)（树根）上的点，我们依旧用之前的方法处理从\(lca\)到\(root\)的路径。
  • 如果要从\(x\)跳到\(fa_x\)，且\(F\)是\(fa_x\)的重儿子，直接加上\(G_x\)即可。
  • 面对一条链上的点，所有点的父亲的重儿子都是该点，则可以直接加上\(\sum G_x\)。
  • 对于一条链上的\(top\)点，它是它的父亲的轻儿子，所以我们应该加上\(F_{fa_x}-F_x-A_x*val_{x,fa_x}\)。

• 以上为大概思路，具体实现应该还有一些细节。

然而值得注意的是，此题的细节极多，需要一定的代码难度。

完整代码：

#include<bits/stdc++.h>
#define LL long long
#define maxn 210000
using namespace std;
int n,m,tag[maxn],last[maxn],p,id[maxn],ID = 0;
int size[maxn],top[maxn],tail[maxn],fa[maxn],son[maxn],type;
LL Dep[maxn],dep[maxn];
LL ans = 0;
struct tree_array
{
    LL d[maxn];
    LL lowbit(LL x) {return x & (- x);}
    LL Insert(int x,LL val) {while(x <= n) {d[x] += val; x += lowbit(x);}}
    LL getsum(int x) {return x ? getsum(x - lowbit(x)) + d[x] : 0;}
    LL query(int l, int r) {if(l > r) swap(l, r); return getsum(r) - getsum(l - 1);}
}A,B,C,D;
struct edge
{
    int x, y, next;
    LL val;
    void Add_edge(int X, int Y, LL Val)
    {
        x = X; y = Y; val = Val;
        next = last[x]; last[x] = p;
    }
}e[maxn * 2];
LL getdis(int u, int v) {return abs(dep[u] - dep[v]);}
LL sumA(int x) {return A.query(id[x], id[x] + size[x] - 1);}
LL sumB(int x) {return B.query(id[x], id[x] + size[x] - 1);}
void init1(int x)
{
    size[x] = 1;
    for(int k = last[x]; k; k = e[k].next)
    if(e[k].y != fa[x])
    {
        int y = e[k].y; fa[y] = x;
        dep[y] = dep[x] + e[k].val;
        Dep[y] = Dep[x] + 1;
        init1(y);
        size[x] += size[y];
        if(size[y] > size[son[x]]) son[x] = y;
    }
}
void init2(int x)
{
    id[x] = ++ ID;
    if(son[fa[x]] == x) top[x] = top[fa[x]];
    else top[x] = x;
    if(son[x]) init2(son[x]);
    for(int k = last[x]; k; k = e[k].next)
    if(e[k].y != fa[x] && e[k].y != son[x])
    init2(e[k].y);
    if(!son[x]) tail[x] = x;
    else tail[x] = tail[son[x]];
}
int LCA(int u, int v)
{
    while(u != v)
    {
        if(Dep[top[u]] < Dep[top[v]]) swap(u, v);
        if(top[u] == top[v]) return Dep[u] < Dep[v] ? u : v;
        else u = fa[top[u]];
    }
    return u;
}
void modify(int x)
{
    tag[x] ^= 1; LL flag = tag[x] * 2 - 1;
    int pos = x;
    A.Insert(id[x], flag);
    B.Insert(id[x], flag * dep[x]);
    while(x)
    {       
        C.Insert(id[x], flag * getdis(pos, x));
        D.Insert(id[x], flag * dep[x]);
        x = fa[top[x]];
    }
}
LL getF(int x) {return abs(sumB(x) - dep[x] * sumA(x));}
void findsum(int x, int anc)
{
    ans += getF(x);
    while(x != anc)
    {
        if(top[x] == top[anc]) {ans += C.query(id[fa[x]], id[anc]); return;}
        else 
        { 
            if(x == top[x]) 
            ans += getF(fa[x]) - getF(x) - sumA(x) * getdis(x, fa[x]);
            else
            {
                ans += getF(fa[top[x]]) - getF(top[x]) - sumA(top[x]) * getdis(top[x], fa[top[x]]);
                ans += C.query(id[fa[x]], id[top[x]]);
            }
            x = fa[top[x]];
        }
    }
}

void Sumlink(int x)
{
    while(x != 1)
    {
        if(top[x] == 1) {ans -= 2 * D.query(id[fa[x]], id[1]); break;}
        else
        {
            if(x == top[x]) {ans -= 2 * ((sumA(fa[x]) - sumA(x)) * dep[fa[x]]);}
            else {
            ans -= 2 * D.query(id[fa[x]], id[top[fa[x]]]);
            ans -= 2 * ((sumA(fa[top[x]]) - sumA(top[x])) * dep[fa[top[x]]]);
            }
            x = fa[top[x]];
        }
    }
}
LL query(int x,int y)
{
    int lca = LCA(x, y); ans = 0;
    findsum(x, lca); 
    findsum(y, lca);
    ans -= getF(lca);
    if(lca != 1)
    {
        ans += sumB(1) - sumB(lca) + (sumA(1) - sumA(lca)) * dep[lca];
        Sumlink(lca);
    } 
    return ans; 
}
int main()
{
    scanf("%d%d%d", &n, &m, &type); 
    for(int i = 1;i <= n - 1;i ++)
    {
        int u,v;LL w; scanf("%d%d%lld", &u, &v, &w);
        e[++ p].Add_edge(u, v, w);
        e[++ p].Add_edge(v, u, w);
    }
    init1(1); init2(1);
    for(int i = 1;i <= n;i ++)
    {
        int opt; scanf("%d", &opt);
        if(opt) modify(i);
    }
    for(int i = 1;i <= m;i ++)
    {
        int opt, x, y;
        scanf("%d%d", &opt, &x);
        if(opt == 2) scanf("%d", &y);
        if(opt == 1) modify(x);
        else printf("%lld\n", query(x, y));
    }
}

记得开\(long long\)哦。

『YQOI2019』失昼城的守星使 题解

原文：https://www.cnblogs.com/dwqhca/p/11412064.html