浅谈树链剖分

本篇随笔讲解图论中的树链剖分相关内容。

树链剖分是树上问题的极常用操作，可以说不会树链剖分，一半以上的树上难题都毫无思路。其重要性不言而喻。想要流畅阅读本篇博客并学习树链剖分，需要读者具有一定的图论基础，并对树形结构和深搜算法有基本的认识。由于本蒟蒻的水平可能不足支持强大的树剖的讲解，所以题解中的一些不足之处敬请大佬们指正。

树链剖分的基本概念

树链剖分，顾名思义，就是把树拆成链。根据树的形态，我们可以很容易的发现，任何一棵树都会有很多条链正好把树完全拆分。但是树链剖分并不是单单地把树拆成链。它拆出的链有“轻重之分”。

那么什么是轻重链呢？

这就涉及到了树链剖分的一些基本概念名词，如下述。

• 重儿子：我们知道，除叶子节点之外，每个节点都会有若干个儿子节点，而只要这个节点不是叶子节点，它都是一棵子树的根。那么，这个父亲节点就有很多个儿子，而一定会有一个儿子的儿子最多，也就是子树最大。那么这个儿子节点就叫做\(x\)的重儿子。
• 轻儿子：与重儿子对照理解，重儿子是唯一的，除了重儿子之外的所有儿子都是轻儿子。
• 重边：父节点与重儿子组成的边（需要注意的是，这里的父节点不一定也是重儿子）
• 轻边：除重边之外的边。
• 重链：由重边连起来的链叫做重链，特别地，一条重链的顶部是一个轻儿子。
• 轻链：由轻边连起来的链叫做轻链。

我们可以通过一张图来直观理解：

树链剖分解决的问题

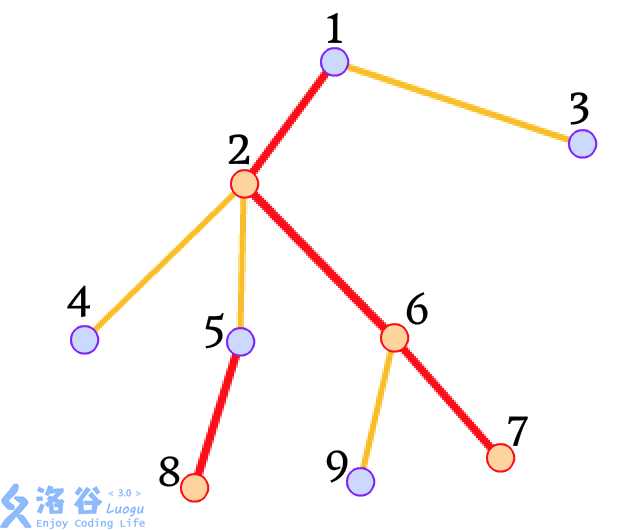
树链剖分是树状结构的操作，自然解决的是树上问题。根据我们以上讲述的基本概念，我们发现我们可以将一棵树进行轻重链的树链剖分。然后我们就可以把一条链上的节点处理成区间的形式（这个理解非常重要！）从而把树上的问题转化成了区间问题进行求解。至于区间问题，我们可以采用一些数据结构求解，比如线段树、树状数组等。

一般来讲，树链剖分可以解决以下问题：

• 修改两点路径上各点的值
• 查询两点路径上各点的值
• 修改某点子树上各点的值
• 查询某点子树上各点的值
• 求解LCA问题

树链剖分的代码实现

根据以上的概念理解，我们会发现，若要求解以上问题，我们用树链剖分的好处就是把树上问题变成区间问题，而区间问题可以用数据结构求解，比如线段树。但是区间需要编号连续，如果用原树的节点编号来进行“区间求解”，那显然是不行的。因为一条链上的节点可能是“3.5.7.8.2.1”这样的乱序，而不是我们想要的一段“连续的数列”，所以这时不能转换成线段树求解。为了让区间连续，我们对整棵树进行预处理。

树链剖分的核心操作也是预处理。

对于任意节点\(x\)，我们通过DFS处理出它的深度，子树大小，重儿子编号和父节点编号。这些东西可以用一次深搜处理出来。实质上就是一个树上遍历的过程。

我们用\(deep[]\)表示深度，\(size[]\)表示子树大小，\(son[]\)表示重儿子是谁（编号），以及\(fa[]\)表示父节点是谁（编号）。

代码：

void dfs1(int x,int f)
{
    fa[x]=f;
    size[x]=1;
    deep[x]=deep[f]+1;
    for(int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(y==f)
            continue;
        dfs1(y,x);
        size[x]+=size[y];
        if(son[x]==0 || size[y]>size[son[x]])
            son[x]=y;
    }
}

但是为了进行树链剖分的相关操作，仅仅处理出这些数据是远远不够的。因为有了这些数据，我们只知道了重链的相关信息，却依然不能维护出我们需要的那段“连续的区间”。所以，我们需要第二遍深搜。

如何在深搜中保证链上节点编号连续呢？

根据深搜的性质和重链的性质，我们已经可以隐隐约约的猜到：用DFS序即可。

也就是说，我们必然会进行第二遍DFS，而第二遍DFS要处理出的东西就是：每条链的顶端节点，每个点的DFS序新编号。

我们用\(top[]\)数组表示每个节点所在链的顶端是谁，\(id[]\)数组表示节点的DFS序新编号。

所以有了以下代码：

void dfs2(int x,int t)
{
    id[x]=++cnt;
    top[x]=t;
    if(!son[x])
        return;
    dfs2(son[x],t);
    for(int i=head[x];i;i=nxt[i])
    {
        int y=to[i];
        if(y==fa[x] || y==son[x])
            continue;
        dfs2(y,y);
    }
}

这里有必要说明一下：

我们先处理重儿子后处理轻儿子。

为什么呢？

因为我们最终的目的是把链的新的DFS编号变成连续的。这样，我们先处理重链再处理轻链，就能做到：每一条重链上的编号是连续的，同时，每一棵子树上的编号也是连续的。

以上就是树链剖分的核心操作：预处理（预处理竟然变成了核心操作）

之后我们回顾一下树链剖分所解决的问题：

• 修改两点路径上各点的值

• 查询两点路径上各点的值

• 修改某点子树上各点的值

• 查询某点子树上各点的值

通过刚才的预处理，我们已经把树上节点的新编号变成了连续的。然后我们就可以针对区间（链）把原树变成线段树来进行我们要做的一系列操作。

所以我们需要把重新编号之后的树的每个顶点映射到这棵线段树上。

浅谈树链剖分

原文：https://www.cnblogs.com/fusiwei/p/11519470.html