K-Means聚类算法不用给出数据集的聚类标签,因此它是一种无监督学习算法,在没有十分明显的分类界限的聚类问题中十分有用。
在聚类问题中我们考虑如下数据集\(\{x^{(1)},\cdots x^{(n)})\}\),我们想要将这些数据点划分到几个集群中,使用K-Means聚类算法的步骤如下:
目标
\[
\begin{align}
\underset{\mu}{min} \underset{C}{min} \sum_{i=1}^{K} \sum_{x \in C_i}|x-\mu_{i}|^2
\end{align}
\]
初始化
随机选取K个点 $ u_{1},u_{2} \dots,u_{k} $ 作为聚类中心,其中K表示聚类个数,该参数由人为设定。
迭代
- 对于每一个样本\(i\), 将样本分配给最近的聚类中心(分配依据:该样本到每个聚类中心的欧式距离):
\[
\begin{align}
c^{i}=arg \underset{j}{min} ||x^{(i)}-u_j||^2
\end{align}
\]
- 对于每一个聚类\(j\),用类内样本的质心更新聚类中心:
\[
\begin{align}
u_{j}=\dfrac{\sum_{i=1}^n 1 \cdot \{c^{(i)}=j \}x^{(i)}}{\sum_{i=1}^n 1 \cdot \{c^(i)=j \} }
\end{align}
\]
结束
当样本和类的所属关系不再改变时结束算法执行。
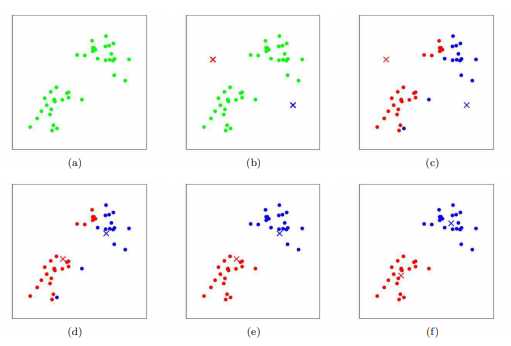
- 如图(a)所示:原始样本集
- 如图(b)所示:随机选择2个聚类中心
- 如图(c)所示:将样本分配给距离最近的聚类中心
- 如图(d)所示:计算类内样本质心更新聚类中心
- 如图(e)所示:跳转执行图(c)的内容
- 如图(f)所示:算法执行结束
K-Means算法
原文:https://www.cnblogs.com/jeapwu/p/11522210.html
