有\(k\)根火柴棒,将这\(k\)根火柴棒恰好用完,能拼出的最小和最大的数分别是多少.
最大的数规律很明显.
对于最小的数,爆搜打表找规律,发现大于某个值之后出现类似循环节的结构.
#include<bits/stdc++.h>
int F[]={6,2,5,5,4,5,6,3,7,6};
long long Ans;
void DFS(long long now,int R,bool Lead)
{
if(R==0)
{
if(now!=0)
Ans=std::min(Ans,now);
return;
}
if(now>Ans)return;
for(int i=0;i<=9;i++)
{
if(Lead&&i==0)continue;
if(R-F[i]>=0)
DFS(now*10+i,R-F[i],0);
}
}
int main()
{
for(int k=2;k<=100;k++)
{
Ans=0x7FFFFFFFFFFFFFFF;
DFS(0,k,1);
printf("%d %lld\n",k,Ans);
}
return 0;
}#include<bits/stdc++.h>
int k;
long long F[105]={0,0,1,7,4,2,6,8,10,18,22,20,28,68,88,108,188,200,208,288,688,888,1088,1888,2008,2088,2888,6888,8888};
int main()
{
freopen("stick.in","r",stdin);
freopen("stick.out","w",stdout);
F[29]=10888;
F[30]=18888;
F[31]=20088;
F[32]=20888;
F[33]=28888;
F[34]=68888;
F[35]=88888;
for(int i=36;i<=100;i++)
F[i]=F[i-7]*10+8;
std::cin>>k;
std::cout<<F[k]<<" ";
if(k%2==1)
{
std::cout<<7;
k-=3;
}
while(k)
{
std::cout<<1;
k-=2;
}
return 0;
}要将一个长为\(l\)宽为\(w\)的矩形木板(厚度忽略)平铺着拖过一个 L 型过道。
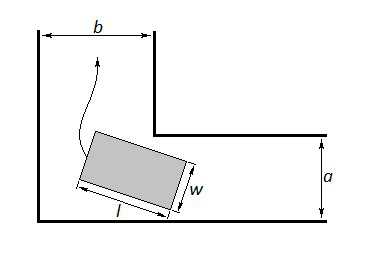
如图所示,L 型过道的两个走廊的宽度分别是\(a\)和\(b\),呈 90°,并且走廊的长度远大于\(l\)。
对于给定的\(a,b,l\),最大的\(w\)是多少,如果无论如何木板都不可能通过,则输出"My poor head =(" .
转化为几何模型.
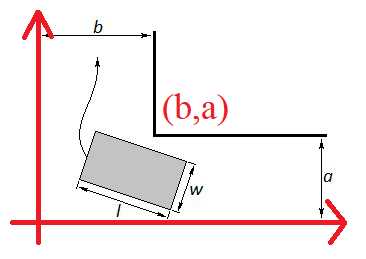
如图,建立直角坐标系,三分横截距,勾股定理计算纵截距,解出直线的方程,计算点到直线的距离.
注意特判某些特殊情况.
#include<bits/stdc++.h>
#define DB double
#define eps (1e-10)
DB A,B,L,Ans;
DB Dis(DB A,DB B,DB C,DB X,DB Y)//点到直线距离
{
DB N=A*X+B*Y+C;
DB M=sqrt(A*A+B*B);
return N/M;
}
int main()
{
std::cin>>A>>B>>L;
if(A-B>eps)std::swap(A,B);
if(B+eps>L)Ans=A;//特判
else
{
DB s=0,e=L;
while(e-s>eps)//三分横截距
{
DB X1=s+(e-s)/3;
DB X2=s+(e-s)/3*2;
DB Y1=sqrt(L*L-X1*X1);//勾股定理计算纵截距
DB Y2=sqrt(L*L-X2*X2);
DB T1=Dis(X1,Y1,-X1*Y1,B,A);//计算点到直线距离
DB T2=Dis(X2,Y2,-X2*Y2,B,A);
if(T1<T2){e=X2;Ans=T2;}
else{s=X1;Ans=T1;}
}
}
if(Ans<-eps)
puts("My poor head =(");
else printf("%.7lf\n",std::min(Ans,L));
return 0;
}C 城所有的道路都是单向的。不同道路之间有路口,每个路口都有一个大楼。
有一天,城市里的所有大楼因为不明原因,突然着火了。作为超人的你要去拯救这些大楼。初始的时候你在 S 号楼,最后你必须到达某个有补给站的大楼,你可以沿着单向道路行驶。你可以经过某条道路或者某个大楼若干次,经过一个大楼你就可以消灭一个大楼的大火。每个大楼都有一个重要程度,最后这个任务的评价分数就是你经过的所有大楼的重要度之和(若重复经过某个大楼多次,则不重复算分)。
你是一个聪明的超人,你想知道,通过合理的规划路线,你这次任务能得到的最高得分是多少。
注意,该城市的道路可能有重边或自环。
Tarjan 缩点,拓扑排序求DAG图上的最短路,时间复杂度\(O(n+m)\).
#include<bits/stdc++.h>
const int SIZE=1000005;
int n,m,head[SIZE],nex[SIZE],fro[SIZE],to[SIZE],Tot,weight[SIZE],S,p;
void Link(int u,int v)
{
nex[++Tot]=head[u];
head[u]=Tot;
fro[Tot]=u;
to[Tot]=v;
}
bool mk[SIZE];
int DFN[SIZE],Low[SIZE],Time,Sta[SIZE],Top;
int Belong[SIZE],Cnt,wx[SIZE],mkx[SIZE];
bool Ins[SIZE];
void Tarjan(int u)
{
DFN[u]=Low[u]=++Time;
Sta[++Top]=u;
Ins[u]=1;
for(int i=head[u];i;i=nex[i])
{
int v=to[i];
if(!DFN[v])
{
Tarjan(v);
Low[u]=std::min(Low[u],Low[v]);
}
else
if(Ins[v])
Low[u]=std::min(Low[u],DFN[v]);
}
if(Low[u]==DFN[u])
{
++Cnt;
do
{
Belong[Sta[Top]]=Cnt;
Ins[Sta[Top]]=0;
wx[Cnt]+=weight[Sta[Top]];
if(mk[Sta[Top]])
mkx[Cnt]=1;
}while(Sta[Top--]!=u);
}
}
int hx[SIZE],nx[SIZE],tx[SIZE],Totx,InDeg[SIZE];
void Linkx(int u,int v)
{
nx[++Totx]=hx[u];
hx[u]=Totx;
tx[Totx]=v;
++InDeg[v];
}
long long Dis[SIZE],Ans;
std::queue<int>q;
int main()
{
freopen("save.in","r",stdin);
freopen("save.out","w",stdout);
scanf("%d%d",&n,&m);
int u,v;
for(int i=1;i<=m;i++)
{
scanf("%d%d",&u,&v);
Link(u,v);
}
for(int i=1;i<=n;i++)scanf("%d",&weight[i]);
scanf("%d%d",&S,&p);
while(p--)
{
scanf("%d",&u);
mk[u]=1;
}
for(int i=1;i<=n;i++)
{
if(!DFN[i])
Tarjan(i);
}
for(int i=1;i<=Tot;i++)
{
if(Belong[fro[i]]!=Belong[to[i]])
Linkx(Belong[fro[i]],Belong[to[i]]);
}
S=Belong[S];
memset(Dis,-0x3F,sizeof(Dis));
Dis[S]=wx[S];
for(int i=1;i<=Cnt;i++)
{
if(InDeg[i]==0)
q.push(i);
}
while(q.size())
{
int u=q.front();
q.pop();
for(int i=hx[u];i;i=nx[i])
{
int v=tx[i];
Dis[v]=std::max(Dis[v],Dis[u]+wx[v]);
--InDeg[v];
if(InDeg[v]==0)
q.push(v);
}
}
for(int i=1;i<=Cnt;i++)
{
if(mkx[i])
Ans=std::max(Ans,Dis[i]);
}
std::cout<<Ans;
return 0;
}原文:https://www.cnblogs.com/TaylorSwift13/p/11523386.html